Problem with the iteration method for finding the roots of a system of equations?

Question

higher mathematics

Hello. My name is Petyr.
The code is written in the WX Maxima environment.
There is a system of nonlinear equations:
f_1(x,y)=sin(x + y) − 1.1x + 0, 2 = 0;
f_2(x,y)=x^2 + y^2 - 1=0;
The graph below shows that this system has four roots

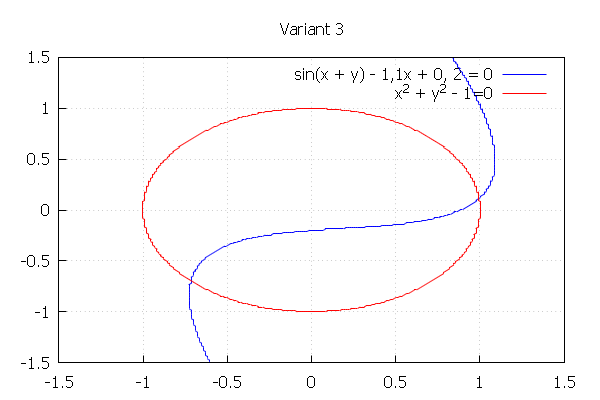
. As an initial approximation, we can take x1 = 1, y1 = 0.5 and x2 = 1, y2 = -1
Let's try to solve our system for x and y:
x = (sin(x+y )-0.1*x+0.2);
y = sqrt(1-x^2);
Let's define the corresponding functions:

g1(x,y):= (sin(x+y)-0.1*x+0.2);
g2(x,y):=sqrt(1-x^2);

Let's set the accuracy and the initial approximation:

x:1; y:0.5; epsilon:10^(−5); n:0;

We start the cycle, the condition for terminating the cycle: the distance between two successive
approximations is less than epsilon.

unless (float(g1(x,y))−x)^2+(float(g2(x,y))−y)^2<epsilon^2 do
(x0:float(g1(x,y)),y0:float(g2(x,y)),x:x0,y:y0,n:n+1);

But in the end, maxima counts for a very long time and does not give an answer. Maybe the problem is in the convergence of functions?
Convergence is guaranteed when

L0 * f(prime)(x)>0, where
L0=1/f(prime)(x0)

L(f1)=-1.657908226985588*del(-0.5) (del - differential)
L(f2) =0.6666666666666669*del(-0.5)

Any help and hint would be appreciated.