How to decompose into irreducible factors in the field R?

Question

Algorithms

Can you tell how approximately it should be done (something like an algorithm?)
Or show some example. They asked me the second one, the last one looks like it, you can use it.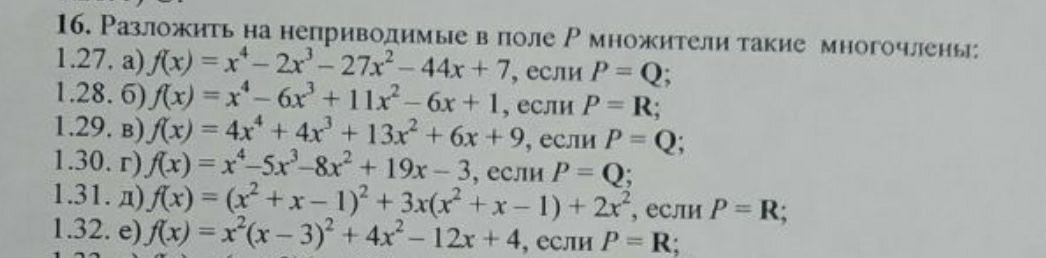
You are welcome

Answer 1

P(x) == (x-x0)*(x-x1)*...., where x0, x1,...- the roots of the polynomial P(x), whose coefficient at the highest term is 1.
You find the roots, if some of them do not belong to the specified fields - you multiply the brackets with them, in the worst case you can get the original polynomial - which means its irreducibility.

Answer 2

First you need to try to find the roots of the polynomial. If there are roots, then divide the polynomial by (x-x0), where x0 is the root, and continue the expansion with the remaining polynomial. If there are no roots, or it is difficult to find, then one should try to find (see) formulas that will somehow simplify or "fold" the expression.
In this case, it may well turn out that there are no roots, but the polynomial is divided into two irreducible polynomials of the form (x^2 + bx + c).
PS.
Estimations in excel show that the polynomial is at least non-negative, and if it has a root, then about the number 0.381966.