Answer the question
In order to leave comments, you need to log in
There is a network address 192.168.01.0, it needs to be divided into 20 subnets with the maximum possible number of nodes. How to choose a mask?
There is a network address 192.168.01.0, it needs to be divided into 20 subnets with the maximum possible number of nodes. How to find a mask?
There are examples of colleagues who have picked up a mask, but I don’t understand how it all
works. I understand that the maximum subnet mask consists of 32 bits.
Here are examples, I don't understand the logic

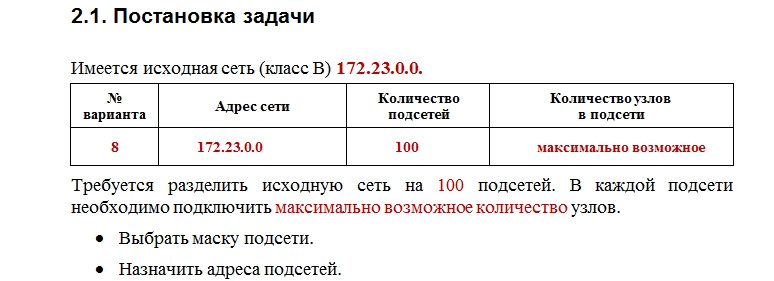

Answer the question
In order to leave comments, you need to log in
Here are examples, I don't understand the logic
For the network address 192.168.1.0, the mask 24 (i.e. 255.255.255.0) is usually used, although it would be nice if the mask was explicitly specified in the task condition.
To divide this subnet into 20 subnets, you need to increase the mask by a few bits. The number 20 can be represented by at least 5 bits. Therefore, we increase the mask by 5 bits. We get the mask 29 (24+5) (i.e. 255.255.255.248). The number of hosts in each of the 32 learned subnets is a maximum of 8 (but since 0 and the last address are broadcast, there are actually 6 of them).
Examples of the resulting subnets:
192.168.1.0/29 - Addresses of hosts: 192.168.1.0 - 192.168.1.7
192.168.1.128/29 - addresses of hosts: 192.168.1.128 - 192.168.1.135
192.168.1.168/29 - addresses of the host: 192.168.168 - 192.168 - 192.168 - 192.168 - 192.168 - 192.168 .1.175
192.168.1.248/29 - host addresses: 192.168.1.248 - 192.168.1.255
There are 32 subnets, not 20, i.e. 12 subnets will not be used. In practice, it usually happens that there are additional conditions. For example, some of the 20 subnets have more than 6 hosts, but most subnets have 2-3 hosts. In this case, you can optimize the subnetting - use not a uniform division (one mask), but a different mask length for different subnets, depending on additional conditions.
The subnet mask is always 32 bits. First there are n ones, then (32-n) zeros. In short, such a mask is written as / n.
And the logic in the examples is the simplest - we take a power of two 2 k , greater than or equal to the required number of subnets and divide the original network with the mask /2 t by the required number. We get the mask /2 t+k .
But the logic is not entirely correct, the task does not say that the subnets should be the same size. In the second example, it was possible to combine (128-100)*2 = 56 subnets in pairs and get 28 subnets with a /22 mask and 72 subnets with a /23 mask.
Didn't find what you were looking for?
Ask your questionAsk a Question
731 491 924 answers to any question