Implementation of the binDCT algorithm. Comparison with conventional DCT. Why different results?

Question

JPEG

Hello,
I'm trying to implement and understand the binDCT algorithm. Found this description. Here is a regular DCT, with an example, on page 3 there is an initial matrix of 8x8 values, and just below is a matrix with calculated values ​​of the DCT coefficients.
To begin with, I try to implement the binDCT algorithm itself (version A) in Python in order to understand the sequence of actions and get at least approximately the same result as in the usual example. The binDCT documentation describes a 1D algorithm, but a two-dimensional matrix must be processed in this order:
1. First, we transform each row according to the algorithm in the circuit.
2. Then, the columns of the matrix obtained as a result of point one are subjected to transformation.
Those. we go through the rows, transpose the matrix, go through the rows again, transpose back
The algorithm itself in the dock (I use version A) can be divided into 7 stages. Shown in the figure .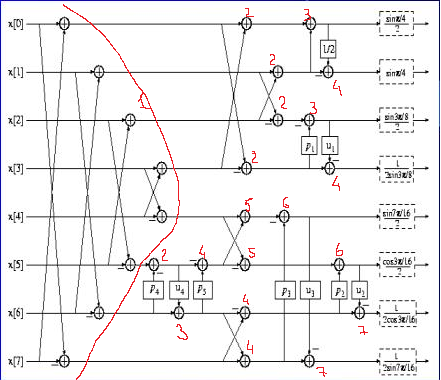
Here is the Python script of this algorithm (it is specially divided into stages and redundant for the convenience of finding errors and quickly replacing the coefficients.)

import numpy as np

M = np.matrix('26 -5 -5 -5 -5 -5 -5 8; 64 52 8 26 26 26 8 -18; 126 70 26 26 52 26 -5 -5; 111 52 8 52 52 38 -5 -5; 52 26 8 39 38 21 8 8; 0 8 -5 8 26 52 70 26 ; -5 -23 -18 21 8 8 52 38; -18 8 -5 -5 -5 8 26 8')

def dct_row (iarray):
   tmp1d1 = np.zeros(8)
   tmp1d2 = np.zeros(8)
   tmp1d3 = np.zeros(8)
   tmp1d4 = np.zeros(8)
   tmp1d5 = np.zeros(8)
   tmp1d6 = np.zeros(8)
   tmp1d7 = np.zeros(8)
   i = 0
   while i <=7:
#stage 1
      tmp1d1[0] = iarray[i,0] + iarray[i,7]
      tmp1d1[1] = iarray[i,1] + iarray[i,6]
      tmp1d1[2] = iarray[i,2] + iarray[i,5]
      tmp1d1[3] = iarray[i,3] + iarray[i,4]
      tmp1d1[4] = iarray[i,3] - iarray[i,4]
      tmp1d1[5] = iarray[i,2] - iarray[i,5]
      tmp1d1[6] = iarray[i,1] - iarray[i,6]
      tmp1d1[7] = iarray[i,0] - iarray[i,7]
#stage 2      
      tmp1d2[0] = tmp1d1[3] + tmp1d1[0]
      tmp1d2[1] = tmp1d1[2] + tmp1d1[1]
      tmp1d2[2] = tmp1d1[1] - tmp1d1[2]
      tmp1d2[3] = tmp1d1[0] - tmp1d1[3]
      tmp1d2[4] = tmp1d1[4]
      tmp1d2[5] = tmp1d1[5] - 0.4375*tmp1d1[6]
      tmp1d2[6] = tmp1d1[6]
      tmp1d2[7] = tmp1d1[7]
#stage 3      
      tmp1d3[0] = tmp1d2[1] + tmp1d2[0]
      tmp1d3[1] = tmp1d2[1]
      tmp1d3[2] = 0.375*tmp1d2[3] - tmp1d2[2]
      tmp1d3[3] = tmp1d2[3]
      tmp1d3[4] = tmp1d2[4]
      tmp1d3[5] = tmp1d2[5]
      tmp1d3[6] = 0.6875*tmp1d2[5] + tmp1d2[6]
      tmp1d3[7] = tmp1d2[7]
#stage 4      
      tmp1d4[0] = tmp1d3[0]
      tmp1d4[1] = tmp1d3[0]*0.5 - tmp1d3[1]
      tmp1d4[2] = tmp1d3[2]
      tmp1d4[3] = tmp1d3[3] - 0.375*tmp1d3[2] 
      tmp1d4[4] = tmp1d3[4]
      tmp1d4[5] = 0.375*tmp1d3[6] - tmp1d3[5] 
      tmp1d4[6] = tmp1d3[7] - tmp1d3[6]
      tmp1d4[7] = tmp1d3[7] + tmp1d3[6]
#stage 5      
      tmp1d5[0] = tmp1d4[0]
      tmp1d5[1] = tmp1d4[1]
      tmp1d5[2] = tmp1d4[2]
      tmp1d5[3] = tmp1d4[3]
      tmp1d5[4] = tmp1d4[4] + tmp1d4[5]
      tmp1d5[5] = tmp1d4[4] - tmp1d4[5]
      tmp1d5[6] = tmp1d4[2]
      tmp1d5[7] = tmp1d4[5]
#stage 6      
      tmp1d6[0] = tmp1d5[0]
      tmp1d6[1] = tmp1d5[1]
      tmp1d6[2] = tmp1d5[2]
      tmp1d6[3] = tmp1d5[3]
      tmp1d6[4] = 0.1875*tmp1d5[7] - tmp1d5[4]
      tmp1d6[5] = 0.875*tmp1d5[6] + tmp1d5[5] 
      tmp1d6[6] = tmp1d5[6]
      tmp1d6[7] = tmp1d5[7]
#stage 7      
      tmp1d7[0] = tmp1d6[0]
      tmp1d7[1] = tmp1d6[1]
      tmp1d7[2] = tmp1d6[2]
      tmp1d7[3] = tmp1d6[3]
      tmp1d7[4] = tmp1d6[4]
      tmp1d7[5] = tmp1d6[5]
      tmp1d7[6] = tmp1d6[6] - 0.5*tmp1d6[5]
      tmp1d7[7] = tmp1d6[7] - 0.1875*tmp1d6[4]

#      
      iarray[i,0] = tmp1d5[0]
      iarray[i,1] = tmp1d5[4]
      iarray[i,2] = tmp1d5[6]
      iarray[i,3] = tmp1d5[2]
      iarray[i,4] = tmp1d5[7]
      iarray[i,5] = tmp1d5[5]
      iarray[i,6] = tmp1d5[3]
      iarray[i,7] = tmp1d5[1]
      
      i = i+1
   return iarray

f = dct_row(M)      
f = f.transpose()
res = dct_row(f)
res = res.transpose()
print res

The DCT coefficients that I get as a result do not come close to the example. Moreover, they are not even multiples.

[1298  114 -122 -122  144 -173  105  121]
[  83   50  -10  -10   54  -57  -23  -46]
[  47  -49   32   32    7  -64   44  -51]
[  47  -49   32   32    7  -64   44  -51]
[ -19   11  -21  -21   14  -16  -37  -67]
[ 122   27   32   32   25  -24   51   88]
[-499  -68  -16  -16  -88  109   41  -81]
[-125   26   35   35   10    5  -14   28]

Tell me what am I doing wrong?