How to solve |x+3| > 6 - |x + 1|?

Question

Mathematics

Good afternoon.
I can't figure out what I'm doing wrong.
I'm trying to solve by the interval method.
Does not work. In the first case - the first interval (from -infinity to -1),
in the first bracket of a different sign, the values ​​\u200b\u200bare obtained by substituting -1 and -5, for example.

Answer 1

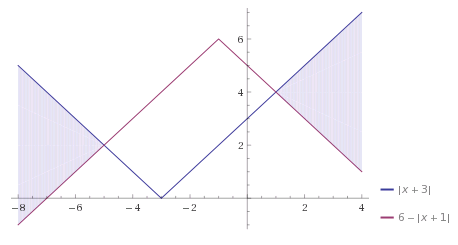
|x+3| > 6 - |x+1|
для поиска точек-пересечений прировняем:
|x+3| = 6 - |x+1|

1) x + 3 = 6 - |x+1|     или     2) x + 3 = |x+1| - 6

1) x + 3 = 6 - |x+1|
-3 + x + |x+1| = 0
|x+1| = 3 - x
x + 1 = 3 - x     или     x + 1 = x - 3
2x + 1 = 3                абсурд
2x = 2                    нет решений
x = 1   (<- одна из точек)

2) x + 3 = |x+1| - 6
9 + x = |x+1|
x + 1 = x + 9     или    x + 1 = -9 - x
абсурд                   2x + 1 = -9
нет решений              2x = -10
                         x = -5   (<- вторая точка)

дальше смотрим где растёт, где падает, мне уже лень

Answer 2

Solve graphically. Draw a left and right graph and highlight the piece when the left is higher than the right.