How to find the optimal path for each pair of elements so that the paths of the connecting lines do not intersect?

Question

Mathematics

Hello.
There is such a picture. When setting pairs: 1-5, 2-9, etc., you need to connect them with lines. Points for possible lines and connections - a square made up of NxN elements, where N is the number of connected elements of one of the connected groups with max. number of elements. You need to connect the lines so that each pair is connected to the other, and there are no dead ends, as with the red lines. In this case, the lines can run either vertically or horizontally, no diagonals.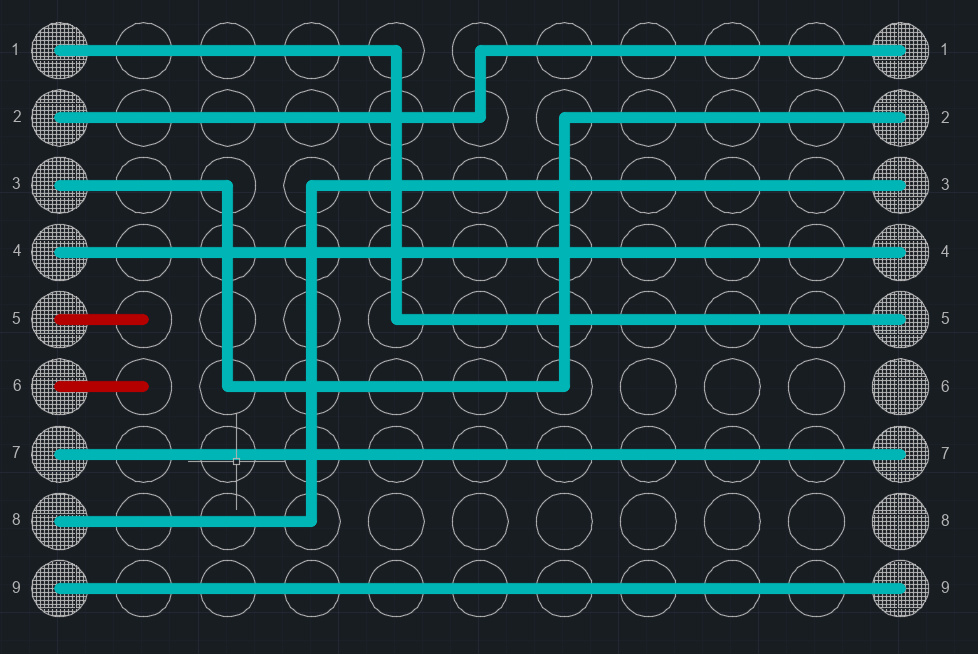

What area of ​​knowledge does drawing belong to, the algorithm of this drawing, the calculation of this most optimal path for each pair of points? What are these algorithms, can I have simple examples for, for example, two groups of elements, 3 on each side?
Specify at least in which direction to look?
PS And, as they correctly corrected me, there is one more condition, I forgot to specify, the lines should not overlap, but they can intersect.
P.S. Amendment. There are no solutions under the specified condition. We add one more condition - the lines can intersect diagonally.

Answer 1

It seems to me that this article can help you (checking the graph for planarity): https://ru.m.wikipedia.org/wiki/%D0%9F%D1%80%D0%BE...
Intersection in your case is the coincidence of transitions from vertex A to vertex B.

Answer 2

the problem in your formulation has no solutions, except for degenerate ones (when everything coincides one to one at once).
firstly, if you need to connect all N elements, then there is no way to avoid deadlocks with red lines, simply because in order to swap a pair of lines you need to have at least one free stripe.
secondly, you have written: "square", and with one free lane, in some cases it will not be enough in length. in order to swap two lines, you need three cells in length: from the first to free temporary, from the second to the first, and modern to the second. so, in the worst case (a lot of lines that need to be swapped in pairs), it's not a square, but a rectangle with an aspect ratio of about two to three.