How to find the angle between the midline and the leg in a triangle?

Question

Mathematics

Good day to all.
I train in Python programming on the Hacker Rank service. I stumbled over the problem of finding an angle in a triangle.

Conditions : a right triangle, a median line is drawn from the right angle to the hypotenuse. The lengths of the legs are known.
Find the angle between the midline and the adjacent leg.


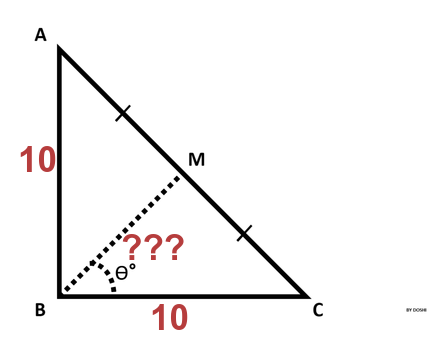
In the discussion to the problem, other participants have already published their solutions. For example:

import math

AB = int(raw_input()) 
BC = int(raw_input()) 
print str(int(round(math.degrees(math.atan2(AB,BC)))))+'°'

The service accepts this code and counts the task, however, I don’t understand where atan2 comes from here ?
I understand that I have a gap in the fundamental knowledge of mathematics. It is not clear to me how the arc tangent is related to this angle at all. I don’t understand what phrase to google for or in which direction to dig at all.

Please point me in the direction.

Answer 1

For starters, this is not your middle line, but the median of the triangle.
From the point M we lower the perpendicular to the side BC. Let's call the intersection point M'.
Consider triangles ABC and MM'C.
∠BCA = ∠M'CM since this is the common angle of the triangles.
∠ABC = ∠MM'C since these angles are right angles.
So these triangles are similar.
CM = 1/2 CA => CM' = 1/2 CB
That is, point M' bisects CB, which means that perpendicular MM' is also the median of triangle BMC.
Hence triangle BMC is isosceles and ∠MBC = ∠BCM = ∠BCA = atan(AB/BC).

Answer 2

Google the ratios in a right triangle.
And the equality of angles in isosceles triangles can come in handy ...
It remains to find where the isosceles triangles are, and they are

Answer 3

How to find an angle on a computer? How can it even be calculated? Very rarely in a problem it is possible to express an angle in terms of some other known angles in degrees. Most often you have some coordinates of some points.
From the coordinates, you can find all trigonometric functions - cosine, sine, tangent ... Then you can already get the angle value in degrees / radians from them through inverse trigonometric functions, for example arctangent (atan in the solution). By definition, it returns the angle if you pass arctangent values ​​to it.
Most often, it is the arc tangent that is used, because, unlike cosines / sines, it works well for any angle (in the arc sine, for example, it is impossible to distinguish between 45 and 135 degrees - the value of the sine is the same). For arcsine and arccosine, you need to add some checks from above to resolve ambiguities.
Why is there such an answer in the problem? atan() is passed the cosine and sine of the angle, possibly stretched by the same factor. The coordinates of the point M are (1/2 AB, 1/2 BC), because this is the midpoint of AC. Imagine a perpendicular from point M to axis OX(BC). The resulting triangle will have a right angle, hypotenuse BM and legs with lengths 1/2 AB, 1/2 BC. Accordingly, the cosine/sine of the desired angle will be 1/2/AM*AB, 1/2/AM*BC. Now remember that atan() can pass values ​​multiplied by a constant. Let the constant be 2/AM. Then AB and BC remain.
Also, you can look at atan() like this - pass it the coordinates of the end of the vector and it will return the angle between OX and the vector.

Answer 4

without multi-letters: the hypotenuse coincides with the median, because two hypotenuses intersect at their midpoints.