How to find angle and vector from rotation matrix?

Question

JavaScript

There is a formula from the book "Fundamentals of Controlling Manipulative Robots" by S.L. Zenkevich, A.S. Yushchenko 2004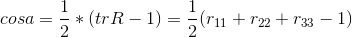

.

.

.

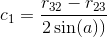
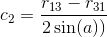
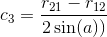
Nagovnokodil, so that it converges with the formulas:
<p id="log"></p>

"use strict";
    // ф-я вывода item(string) внутри тега p с id "log"
    var log = function(item) {
      var p = document.getElementById("log");
      Array.isArray(item) ? item.forEach(function(current, i, array) {
        log("[" + current + "]")
      }) : p.innerHTML += item + "<br />"
    };
    var calcAngleAxisFromRotateMatrix = function(rotateMatrix) {
      var R = rotateMatrix,
        cosA = (1 / 2) * (math.subtract((R[0][0] + R[1][1] + R[2][2]), 1)),
        angleRad = math.acos(cosA),
        sinA = math.sin(angleRad),
        sinAx2 = 2 * sinA,
        axis = [(R[2][1] - R[1][2]) / sinAx2, (R[0][2] - R[2][0]) / sinAx2, (R[1][0] - R[0][1]) / sinAx2];
      return [angleRad, axis]
    };
    var AngleAndAxis = calcAngleAxisFromRotateMatrix([
      [1, 0, 0],
      [0, -1, 0],
      [0, 0, 1]
    ]);
    log(AngleAndAxis[0] * 180 / Math.PI); // angle
    log(AngleAndAxis[1]); // angle

Input - matrix - function argument calcAngleAxisFromRotateMatrix
https://jsfiddle.net/Quncore/1kfsL0b5/
For the rotation matrix around the X and Z axes by 90 and 180 degrees, respectively, the angle is determined, but not the axis. For an angle of 30 degrees, the denominator is 0, so the calculations do not go.
The following matrices were used for the test:

R90x
[1,0,0]
[0,0,-1]
[0,1,0]
R30y
[1,0,0]
[0,1,0]
[0,0,1]
R180z
[-1,0,0]
[0,-1,0]
[0,0,1]

Answer 1

Rotation matrices:
----------- in Z
cos(a) sin(a) 0 0
-sin(a) cos(a) 0 0
0 0 1 0
0 0 0 1
----- ------ X
1 0 0 0
0 cos(a) sin(a) 0
0 -sin(a) cos(a) 0
0 0 0 1
----------- Y
cos(a) 0 -sin(a) 0
0 1 0 0
sin(a) 0 cos(a) 0
0 0 0 1