Answer the question
In order to leave comments, you need to log in
Why does the basic trigonometric identity always work?
In the 8th grade, we went through the basics of trigonometry, now I'm in 9th, and I had this question: how to find the sine, cosine and tangent of an arbitrary non-rectangular triangle, I used the theorem
The square of each side of a triangle is equal to the sum of the squares of the other two sides without doubling the product of these sides by the cosine of the angle between them
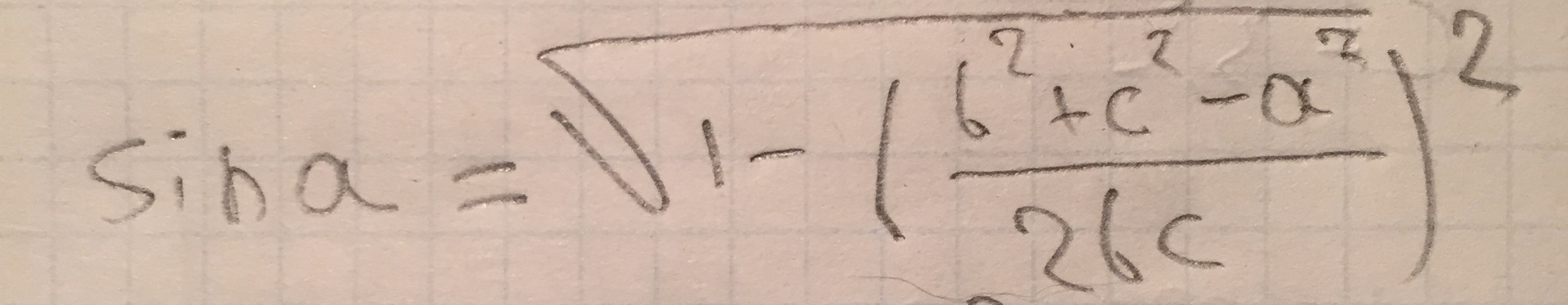
Answer the question
In order to leave comments, you need to log in
> why does OTT work here if it is proved using the Pythagorean theorem?
From the order in which you apply the proved theorems, their truth does not change. OTT - proven for any angle value. Everything, regardless of whether you are counting something in a triangle, or the matrix of turning the plane by a given angle, or counting the area of your piece of the pie.
OTT always applies! For any arguments. But, perhaps this is what confused you, after applying OTT and taking the root, in theory, you will get +-sqrt(...). Because x^2=9 => x=3 or -3. Two options for extracting the root, 2 options for the sinus.
But since you know that an angle in a triangle cannot exceed 180 degrees, you know that the sine of that angle is always non-negative. Therefore, -sqrt() can be discarded as an extra value and get your formula. In a formal proof, these considerations must be taken into account.
Didn't find what you were looking for?
Ask your questionAsk a Question
731 491 924 answers to any question