Answer the question
In order to leave comments, you need to log in
How to check if a point on a plane belongs to a specified part of a circle?
The initial data are as follows: there are points A and B, their coordinates are known. A line of length \u003d X, coming from point A, and passing through point B, is the radius of the circle. The angle between this line and the line that cuts off part of such a circle is Y. (the second line has exactly the same Y angle). How can one test an arbitrary point for belonging to this part of the circle, which is cut off by two such lines?
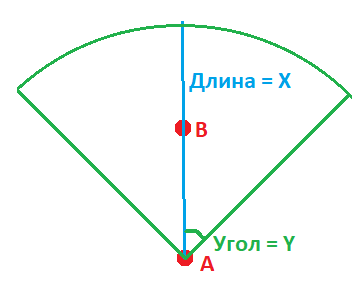
Answer the question
In order to leave comments, you need to log in
First, check that the point lies inside the circle (just compare the distance to A).
Secondly, it is necessary to check that the point lies in the sector. There are 2 options here. You can get the angles of the borders and the direction to the point through the arc tangent and compare, but there are many special cases, especially when passing through 0. An alternative is to use vectors. Let the desired point be P. Then you need to check that the vector AP makes an angle less than y with the vector AB. You can find the cosine of an angle using the scalar product and then compare it with the cosine of y.
You want (AB,AP)/(|AB|*|AP|) >= cos y
Didn't find what you were looking for?
Ask your questionAsk a Question
731 491 924 answers to any question