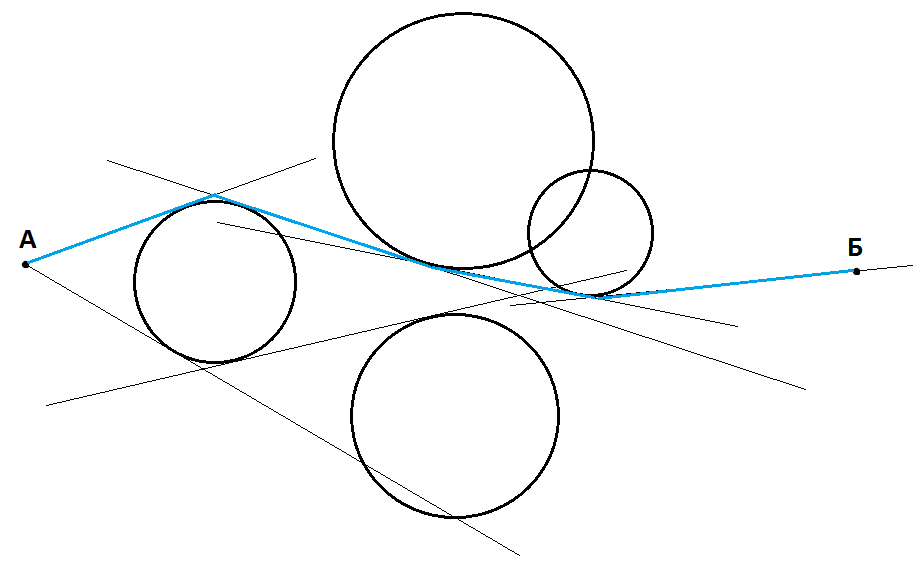
What is the best way to find a path among circles?

Question

Algorithms

- On a flat space there are a huge number of circles of two types:
a) impassable
b) slow down the movement 3 times inside themselves
- Circles are not constant, i.e. may appear or disappear over time (the option with a level designer and manual construction of the graph for A* is no longer needed)
- Circles can intersect.
- Circles have any radius, both small and very large.
- The character represents a dimensionless point.
- All dimensions (coordinates, radii) are real.
How to find an almost optimal path from point A to point B for a specific point in time, consisting of segments (broken line)?

spoiler

spoiler

spoiler

Answer 1

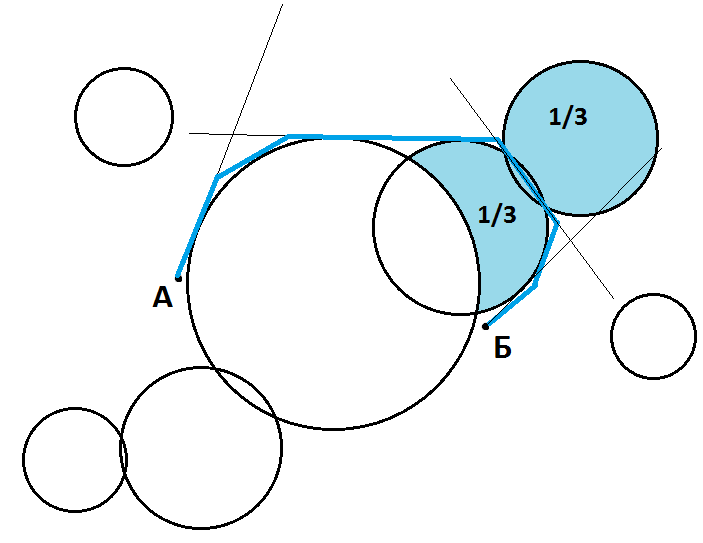
It is easy enough to prove that the paths will lie along common tangents and arcs between tangent points for impassable spheres. You can build a dynamic graph and use A*.
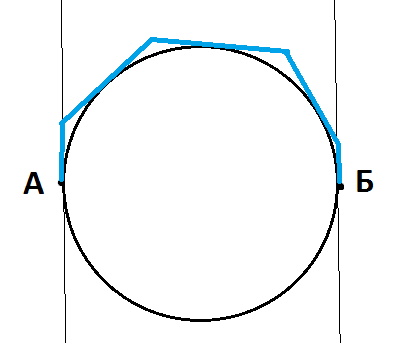
With braking circles it can be more difficult. If they cannot intersect with obstacles, then it is more profitable to bypass them along an arc that is no more than pi/2 (~1.5) longer than the chord.
If they can, then if it is difficult to find an analytical solution, I would add a few points on the boundary of the slow zones to the graph and look for an approximate solution.
About impassable circles: https://redblobgames.github.io/circular-obstacle-p...

Answer 2

- Circles are not constant, i.e. may appear or disappear over time

Are there options that a circle may appear around the character, and he will not be able to move at all?
Or will a group of circles create an impenetrable contour around the character?