How to implement an exact algorithm for the correct coloring of the edges of a graph?

Question

Programming

We need to find the chromatic index of the graph. So far, I have implemented only an inexact algorithm by searching for the degrees of the vertices of the graph, sequentially choosing the vertex with the maximum degree and coloring the incident edges of the selected vertex in different colors, while there are still uncolored ones.
That's why it is not accurate, which gives only the most approximate chromatic index.
Here is an example of his mistake, he paints with 5 colors: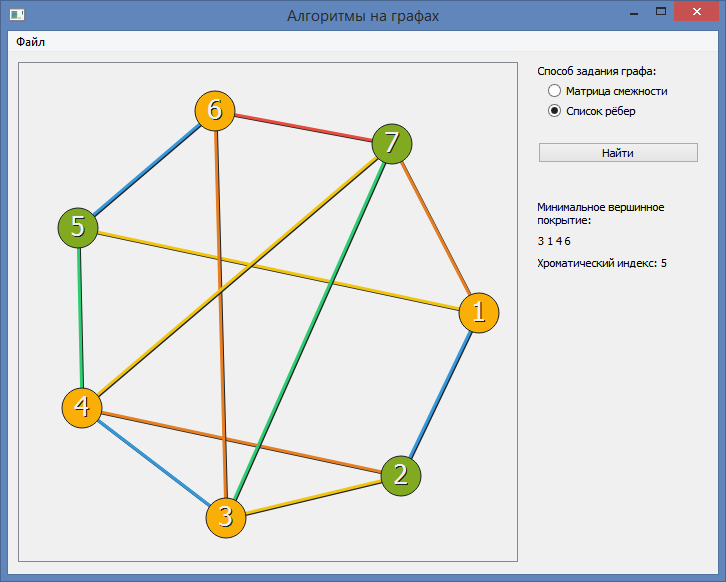

Although it is possible with 4: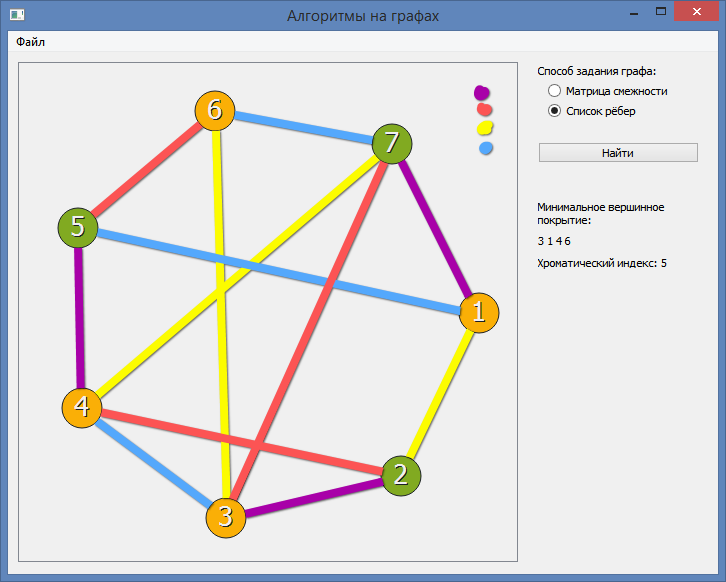

How to implement the exact algorithm for the correct coloring of the edges of the graph? Hitting the forehead with a search of all colors is not an option. We need something faster and more algorithmic. I don’t have any ideas myself, or rather I had them, but they are also inaccurate. I tried to google, I didn’t find anything normal for coloring edges, only for coloring vertices.

Answer 1

There are polynomial time algorithms that produce an optimal coloring of bipartite graphs and a coloring of a simple non-bipartite graph with {\Delta}+1 colors.

So, you can find a coloring in Delta + 1 colors in polynomial time (which may not be fast at all). But to prove that there is no coloring (otherwise, find one) exactly in Delta colors, it is necessary to solve the NP-complete problem in exponential time.
(Delta is the maximum degree of the vertex).