Projective transformation (search for the relative position of a point)

Question

Programming

Good afternoon.
I am now trying to figure out this problem:
Given: a regular quadrilateral and a square, which are given by their coordinates A(x1,y1), B(x2,y2), C(x3,y3), D(x4,y4) and M(0 ,0), N(1,0), P(1,1), K(0,1), respectively.
There is a point P(x,y) that is in this quadrilateral.
Required: Build a projective transformation matrix to transform ABCD into a square MNPK. Next, you need to find the position of the point P`(x`,y`) in the square.
I figured out the construction of the matrix (most likely, I'm doing it right):
I derived the formulas for finding the transformation matrix from a square to a quadrilateral: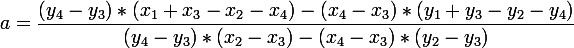
.
.
.
.
.
.
.
.
.
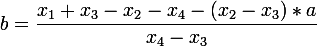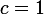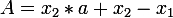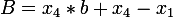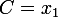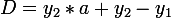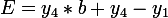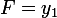I get the matrix: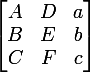

After that, thanks to Habrauser @Mrrl , I find the inverse matrix (by the Gauss method).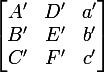

Next, I'm trying to get the coordinates of a point in a square given the coordinates of a point in a quad: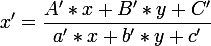
.

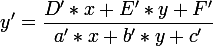
But I'm getting the wrong answer. I substitute completely different points, but I get x and y 0.5.
I am sure that the algorithm for finding the inverse matrix works correctly (I checked the results with online services).
I am also confident in the construction of the matrix, substituting a specific x1, y1, x2, y2, x3, y3, x4, y4 and solving the system, I received the same answers on the sheet and in the program.
Where did I go wrong? What am I doing wrong?
You can't do without a fresh look .
Example:
Given:
A (CP[1]) {x=0 y=0 }
B (CP[2]) {x=1 y=0 }
C (CP[3]) {x=2 y=2 }
D (CP[4]) {x=0 y=1 }
Direct matrix:
{0.666666666666666674 , 0.00000000000000000, -0.33333333333333331}
{0.00000000000000000, 0.66666666666666663, -0.33333333333333337}
{0.00000000000000000, 0.00000000000000000, 1.0000000000000000}
The inverse matrix:
{1.4999999999999998, 0.00000000000000000, 0.49999999999999994}
{-0.00000000000000000, 1.5000000000000000, 0.50000000000000011}
{-0.00000000000000000, -0.00000000000000000, 1.0000000000000000}
thank you all , everything worked correctly.
The problem was in the processing of the received data.
There was a typo when accessing the array, and the Points[i+2] element was taken, but Points[i*2] is needed.
Moral: No need to write code at night)

Answer 1

And can you write the obtained direct and inverse matrices for some example? For example, for A=M, B=N, D=K, C=(2,2) ?