I am looking for an algorithm for analyzing non-trivial data

Question

Mathematics

The context of the question relates to sound and psychoacoustics. But the question itself is related to information and algorithms.

First, a very brief description of the context. The note spectrum of a "normal" musical instrument consists of
individual lines (harmonics) that form an arithmetic progression in frequency



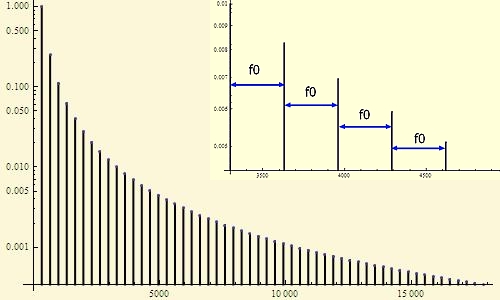
and fall off approximately as ~1/f in amplitude. (“Normal” means: not bells, and not even a pan flute).
Several notes played at the same time (chord) form a "moire pattern" of harmonics:



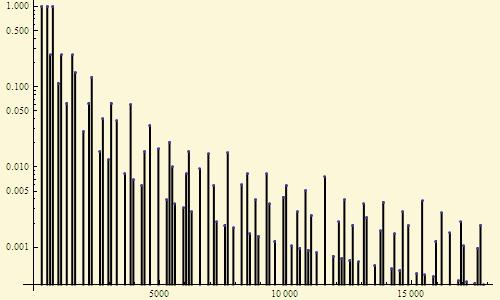
I deal with the topic of consonance / dissonance, i.e. the degree of "pleasantness" of the sound of the chord.
There are several hypotheses about how the shape of the spectrum affects the consonance.

One of them has much more to do with information and algorithms than acoustics.
It is argued that one of the ways that the auditory cortex (and even more so the frontal)
analyzes sound iscognitive, i.e. the spectrum is perceived as a whole and the brain selects
the "description algorithm" of the line pattern.
If this algorithm is simple, compact, then the chord is perceived as pleasant, consonant.
If the algorithm turns out to be "fancy", then the sound is evaluated as non-musical,
ugly. Obviously, we are talking about the so-called. Kolmogorov complexity.

At the level of description, I liked this hypothesis. But I would like to get quantitative estimates!
It can be simplified to say that for any complex sounds, our hearing instinctively tries to pick up one tone.
In this way, one can try to estimate how close the complex pattern of a chord is to a series of harmonics of a single note.

The problem is that experiments show that the fundamental frequency of a "virtual note" may
not belong to the chord at all!
This is where I started to slow down. And the question is like this.
There is a data set of the form {{f1, a1}, {f2, a2}, .....}, where f are frequencies and are amplitudes.
- We need an algorithm for estimating how close this set is to the harmonic {{f0, a0}, {2*f0, a0/2}, {3*f0, a0/3}, ....} with some (previously unknown) f0 .
- Or, a quantitative assessment of the algorithmic complexity of the original set.

I apologize for some confusion, I'm ready to clarify the details.

Answer 1

The first thing that comes to mind is a wavelet decomposition using a suitable parent wavelet (for example, in the form of a note spectrum), after which just look at the coefficients.

Answer 2

I've come up with a very primitive analysis. For a note, all distances between lines are the same,
i.e. their (distance) variance is zero. You can take all pairwise distances between lines in a chord as a data set, and calculate all its stats. data - variance, symmetry, etc.

Answer 3

> I deal with the topic of consonance / dissonance, i.e. the degree of "pleasantness" of the sound of the chord.
If I am not mistaken, it does not depend on the ratio of the amplitudes of the harmonics, but on the ratio of the frequencies of the notes included in it.
Do you know about the ratio of the frequencies of notes (meaning the main frequency) in consonant and dissonant combinations? This is what Pythagoras did. For example, if the notes differ by 12 semitones, then this ratio is 2:1, if by 7 pt then 3:2, if by 5 pt then 5:4 (like so?). Such "multiple notes" have many harmonics that coincide with each other. They sound like they merge.
Let's take the opposite example: notes that differ by 1 pt. In a combination of such notes, if you depict the spectrum, the harmonics do not match, they look like double sticks, they are close to each other and they do not sound very pleasant.
In a major chord, there are also some relationships between the frequencies of the sound of individual notes.
Also, I have a feeling that the brain can combine harmonics with the fundamental frequency. For example, the sounds of musical instruments are made up of harmonics, but we hear them as one note, not several. Therefore, probably, the amplitude of individual harmonics (and the nature of their change in time) determines the timbre of the sound, but not the “pleasantness” of the sound of the chord.