How to recognize a complex geometric object close to an oval?

Question

Python

There is a complex geometric figure.

It needs to be filled with red.
The following criteria are known:
1. This is, in theory, the only closed area in the image. (maybe another one).
2. It does not touch the borders of the image.
3. It is remotely oval, maybe in the form of a pinched oval (sorry for the terms).
I tried the Hough transform (an example with the search for circles), the option did not work.
Here we get 2 questions:
1. Is it possible to use neural networks for this task, if so, what specific type? Examples will dial a maximum of 20 different pieces.
2. Are there algorithms or methods that make it possible to understand closedness (except for a beetle) and an approximately oval shape?
PS I write in Python and C++. In Google, it only throws on articles with a beetle and Hough. Please help.

Answer 1

I will type a maximum of 20 different examples

Much more is needed to train a neuron. Write a heuristic.
Since the area does not touch the edge - fill the image from the point on the border, and your area will be unfilled.
If there are several closed areas, but you need to choose one, you need an ovality criterion. Come up with some. For example: we draw an ellipse of equal area over the area, minimizing the area of ​​"capes" and "peninsulas" protruding beyond the ellipse. This is a simple task to find the minimum, the parameters - well, it's clear what the parameters of the ellipse are) Well, let's see which area is less clumsy.

Answer 2

The closedness of the contour can only be determined by going through the entire contour, so it does not matter here the Beetle or Chuchundra.
But the definition of similarity to an oval, in theory, can be combined with bypassing the contour.
In SOPROMAT there are formulas for determining the main axes of inertia, in the case of an ellipse they coincide with the axes of the ellipse, there is also a formula for determining the center of mass.
For example, here:
www.toehelp.ru/theory/sopromat/18.html
Everything is based on integrals, but in our case, you can simply replace it with sums.
The algorithm is as follows: we find a closed contour, we find the center of mass (from the coordinates of the points of the found contour), we find the main axes of inertia (similarly from the coordinates), we find the area of ​​\u200b\u200bthe contour (here you can sum the area of ​​triangles formed by the center of mass (inertia) and two successive points contour).
Further, having the center of mass and the direction of the axes of inertia, find the semiaxes of the ellipse (this can be done by releasing rays from the center of mass in the direction of the main axes of inertia until they intersect with the contour), and knowing the semiaxes, we find the area of ​​the ellipse.
Next, we compare the areas of two figures: the original and the ellipse - for example, you can take the ratio of areas and compare it with unity.
You need to formulate the similarity criterion yourself based on the conditions of the problem, but since If you have a large test sample, you can use it to calculate the ratio of the area of ​​contours and their ellipses for all cases and take the average value.
Of course, there are a lot of operations here, but it is much simpler and not as costly in terms of resources as neural networks.

Answer 3

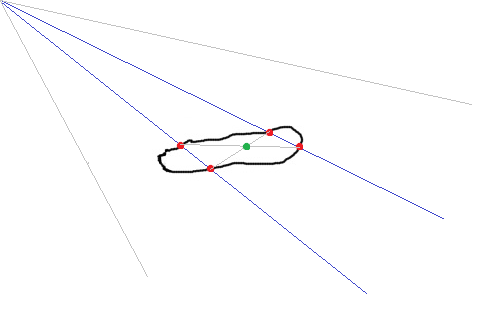
1. We rotate the beam from the corner of the image and save all intersections with the contour.
2. We are looking for close groups of 4 points
3. We check that the diagonals of the irregular 4-gon do NOT intersect with the contour.
4. We look at the ratio of the distances of the group of these points to each other.

Answer 4

https://en.wikipedia.org/wiki/Hough_transform
scikit-image.org/docs/dev/auto_examples/edges/plot...