Answer the question
In order to leave comments, you need to log in
How to project a figure onto a plane?
Hello!
I can't figure out how to project a figure onto a plane.
Let's say I define a quadrilateral in the XYZ plane with points:
A = (x1,y1,z1)
B = (x2,y2,z2)
C = (x3,y3,z3)
D = (x4,y4,z4)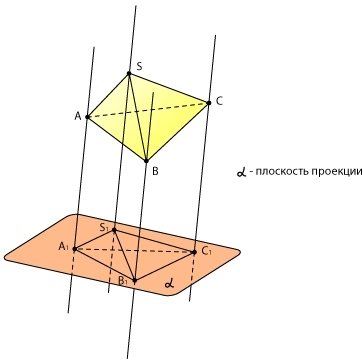
Answer the question
In order to leave comments, you need to log in
But I can't figure out how, having a point with coordinates (x, y, z), translate into (x, y)
To find a point "in the plane", you need to define a coordinate system in it. That is, choose the origin point O(x0,y0,z0) and two basis vectors X=(x1,y1,z1) and Y=(x2,y2,z2). From what you say about "Cartesian coordinate system", the vectors should be of unit length and perpendicular to each other.
You add a Z vector to the system, in parallel to which the design is going on. From the condition it is not clear whether you are considering only an orthogonal projection, or the general case of a parallel projection.
In the case of orthogonal, everything is simple - you don’t even need to mess with matrices:
the vector Z is calculated as the vector product of X and Y, but we don’t need it at all: if the projected point P has coordinates (x, y, z), then its projection Q will have coordinates (in plane coordinate system)
x'=(PO,X)=(x-x0)*x1+(y-y0)*y1+(z-z0)*z1
y'=(PO,Y)=(x-x0)*x2+(y-y0 )*y2+(z-z0)*z2.
In the case of an oblique projection, the calculations are more complicated - you need to multiply the vector (PO) by the matrix inverse to the matrix composed of X,Y,Z. And there the main thing is not to get confused, where are the rows and where are the columns.
I didn’t quite understand the question, I want to clarify: is the plane on which you want to make a projection - is it an arbitrary plane or does it mean a plane formed by the coordinate axes (xy yz xz)?
because if the second - it turns out everything is trite. You just take the coordinates of the same points, place them on the plane. Visibility is determined by the Z coordinate. In this case, this is redundant information, because you are simply projecting a flat figure onto a plane.
Write in the comment if you did not quite understand me or I misunderstood you
Didn't find what you were looking for?
Ask your questionAsk a Question
731 491 924 answers to any question