How to plot a polynomial trend?

Question

Mathematics

Good afternoon. It was necessary to make an approximation by a polynomial of the mth degree. At the input there is an array with data, at the output we get the coefficients of the approximating polynomial of the mth degree
F(x) = a0+a1*x+a2*x^2+...+am*x^
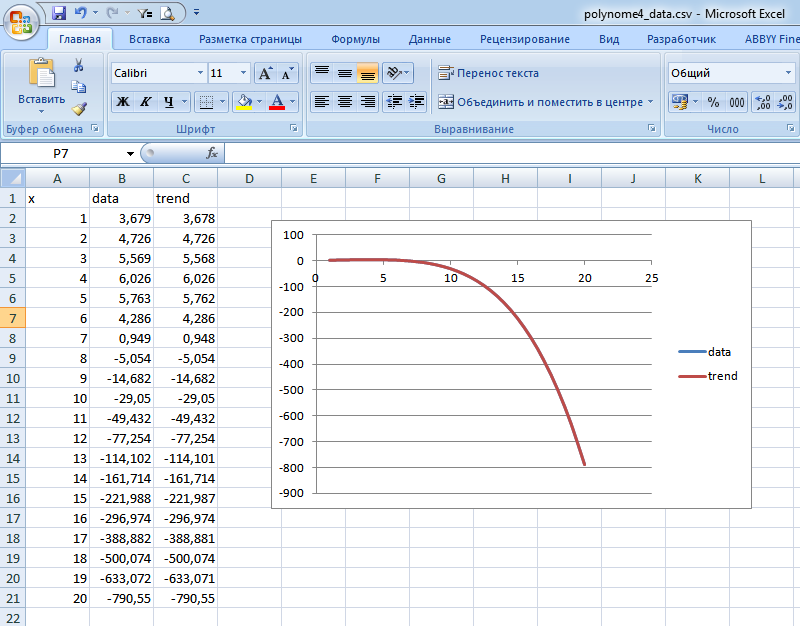
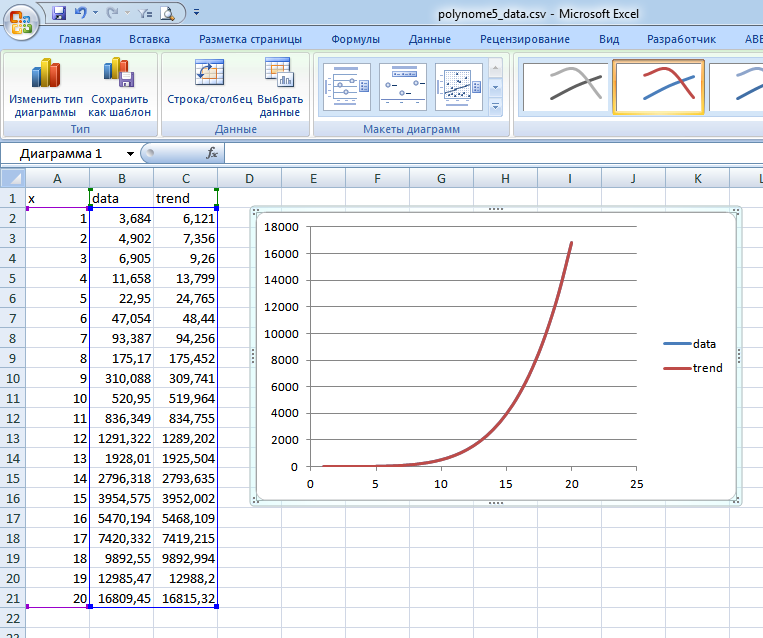
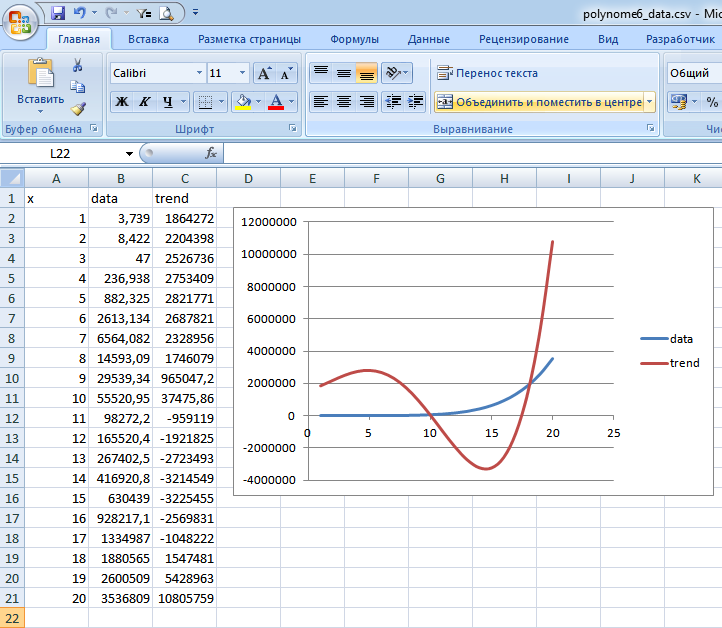
m Made a universal function that counts. Up to the 4th degree, inclusive, everything works perfectly - the data (when generated by function) coincides 1 to 1. At the 5th degree, deviations begin, and the 6th degree is no good. Moreover, all this is considered by the same function, only with a different parameter m.

Screenshots and charts

Вот для 4й степени:

Вот для 5й степени:

Вот для 6й степени:

What could be the problem? I suspect the double accuracy limit , matrices are formed there and multiplied, the error may accumulate.
The code:

The code

private static IList<double> GetPolynomeTrend(IList<double> candles, int period, int m)
  {
    int N = candles.Count;
    int num = N - period;
    if (num < 0) num = 0;
    
    if ((N-num)<=m)//Проверка на длину массива и m
    {
      throw new ArgumentException("Data length must be large of degree of the polynomial (Длинна данных должна быть больше размера полинома)");
    }
    // http://simenergy.ru/math-analysis/digital-processing/85-ordinary-least-squares
    // 1. Начальные данные:
    // - задан массив экспериментальных данных с количеством измерений N
    // - задана степень аппроксимирующего многочлена (m) 
    // 2. Алгоритм вычисления:
    // 2.1. Определяются коэффициенты для построения системы уравнений размерностью m+1
    //double[,] c = new double[m + 1, m + 1]; // коэффициенты системы уравнений (левая часть уравнения) 
    Matrix c = new Matrix(m + 1, m + 1);	  // коэффициенты системы уравнений (левая часть уравнения) 
    for (int k = 1; k <= (m + 1); ++k)
      // k - индекс номера строки квадратной матрицы системы уравнений 
      for (int j = 1; j <= (m + 1); ++j)
        // j - индекс номера столбца квадратной матрицы системы уравнений 
        for (int i = num+1; i <= N; ++i)
        { 
          c[k - 1, j - 1] += Math.Pow(i, (k + j - 2)); //x[i]==i+1, т.к. x-просто индекс
        }
    c.Print("c");

    Matrix d = new Matrix(m + 1 , 1); //  свободные члены системы линейных уравнений (правая часть уравнения) 
    for (int k = 1; k<=(m+1); ++k)
      // k - индекс номера строки квадратной матрицы системы уравнений 
      for (int i = num+1; i<=N; ++i) //for (int i = 1; i<N+1; ++i) 
      {
          d[k - 1, 0] += candles[i - 1] * (Math.Pow(i, (k - 1))); //x[i]==i+1, т.к. x-просто индекс
      }
    d.Print("d");
    // 2.2. Формирование системы линейных уравнений размерностью m+1.
    // |c[1,1] ... c[1,j]| |a0| |d1|
    // |  ...  ...   ... |*|..|=|..|
    // |c[k,1] ... c[k,j]| |am| |dn|
    Matrix a = new Matrix(m + 1 , 1);
    // 2.3. Решение системы линейных уравнений с целью определения неизвестных коэффициентов аппроксимирующего многочлена степени m.
    Matrix cInv = c.CreateInvertibleMatrix();		cInv.Print("c^-1");

    a = cInv * d;		a.Print("a");
    
    int count = candles.Count;
    double[] numArray = new double[count];
    for (int i = num; i < count; ++i)
      for (int pow = 0; pow <= m; ++pow)
      { 
        numArray[i] += a[pow,0] * (Math.Pow(i+1, pow));
      }
    return (IList<double>)numArray;
  }

Matrix class: (hence - github )
I added lines 92-95, otherwise it crashed

if (this.N == 1)
    {
      return this[0, 0];
    }

spoiler

using System;

public class Matrix
{
  private double[,] data;
  private double precalculatedDeterminant = double.NaN;

  private int m;
  public int M { get => this.m; }

  private int n;
  public int N { get => this.n; }

  public bool IsSquare { get => this.M == this.N; }

  public void ProcessFunctionOverData(Action<int, int> func)
  {
    for (var i = 0; i < this.M; i++)
    {
      for (var j = 0; j < this.N; j++)
      {
        func(i, j);
      }
    }
  }

  public static Matrix CreateIdentityMatrix(int n)
  {
    var result = new Matrix(n, n);
    for (var i = 0; i < n; i++)
    {
      result[i, i] = 1;
    }
    return result;
  }

  public Matrix CreateTransposeMatrix()
  {
    var result = new Matrix(this.N, this.M);
    result.ProcessFunctionOverData((i, j) => result[i, j] = this[j, i]);
    return result;
  }

  public Matrix(int m, int n)
  {
    this.m = m;
    this.n = n;
    this.data = new double[m, n];
    this.ProcessFunctionOverData((i, j) => this.data[i, j] = 0);
  }

  public double this[int x, int y]
  {
    get
    {
      return this.data[x, y];
    }
    set
    {
      this.data[x, y] = value;
      this.precalculatedDeterminant = double.NaN;
    }
  }

  public void Print(string matrixName)
  {
    //return;
    Console.Out.WriteLine("\nMatrix "+ matrixName);
    for (int i = 0; i < this.m; i++)
    {
      Console.Out.Write("( ");
      for (int j = 0; j < this.n; j++)
        Console.Out.Write(this.data[i, j] + "\t");
      Console.Out.WriteLine(" )");
    }
  }
  public double CalculateDeterminant()
  {
    if (!double.IsNaN(this.precalculatedDeterminant))
    {
      return this.precalculatedDeterminant;
    }
    if (!this.IsSquare)
    {
      throw new InvalidOperationException("determinant can be calculated only for square matrix");
    }
    if (this.N == 2)
    {
      return this[0, 0] * this[1, 1] - this[0, 1] * this[1, 0];
    }

    if (this.N == 1)
    {
      return this[0, 0];
    }

    double result = 0;
    for (var j = 0; j < this.N; j++)
    {
      result += (j % 2 == 1 ? 1 : -1) * this[1, j] * 
        this.CreateMatrixWithoutColumn(j).CreateMatrixWithoutRow(1).CalculateDeterminant();
    }
    this.precalculatedDeterminant = result;
    return result;
  }

  public Matrix CreateInvertibleMatrix()
  {
    if (this.M != this.N)
      return null;
    var determinant = CalculateDeterminant();
    if (Math.Abs(determinant) < Constants.DoubleComparisonDelta)
      return null;

    var result = new Matrix(M, M);
    ProcessFunctionOverData((i, j) => 
    {
      result[i, j] = ((i + j) % 2 == 1 ? -1 : 1) * CalculateMinor(i, j) / determinant;
    });

    result = result.CreateTransposeMatrix();
    return result;
  }

  private double CalculateMinor(int i, int j)
  {
    return CreateMatrixWithoutColumn(j).CreateMatrixWithoutRow(i).CalculateDeterminant();
  }

  private Matrix CreateMatrixWithoutRow(int row)
  {
    if (row < 0 || row >= this.M)
    {
      throw new ArgumentException("invalid row index");
    }
    var result = new Matrix(this.M - 1, this.N);
    result.ProcessFunctionOverData((i, j) => result[i, j] = i < row ? this[i, j] : this[i + 1, j]);
    return result;
  }

  private Matrix CreateMatrixWithoutColumn(int column)
  {
    if (column < 0 || column >= this.N)
    {
      throw new ArgumentException("invalid column index");
    }
    var result = new Matrix(this.M, this.N - 1);
    result.ProcessFunctionOverData((i, j) => result[i, j] = j < column ? this[i, j] : this[i, j + 1]);
    return result;
  }

  public static Matrix operator *(Matrix matrix, double value)
  {
    var result = new Matrix(matrix.M, matrix.N);
    result.ProcessFunctionOverData((i, j) => result[i, j] = matrix[i, j] * value);
    return result;
  }

  public static Matrix operator *(Matrix matrix, Matrix matrix2)
  {
    if (matrix.N != matrix2.M)
    {
      throw new ArgumentException("matrixes can not be multiplied");
    }
    var result = new Matrix(matrix.M, matrix2.N);
    result.ProcessFunctionOverData((i, j) =>
    {
      for (var k = 0; k < matrix.N; k++)
      {
        result[i, j] += matrix[i, k] * matrix2[k, j];
      }
    });
    return result;
  }

  public static Matrix operator +(Matrix matrix, Matrix matrix2)
  {
    if (matrix.M != matrix2.M || matrix.N != matrix2.N)
    {
      throw new ArgumentException("matrixes dimensions should be equal");
    }
    var result = new Matrix(matrix.M, matrix.N);
    result.ProcessFunctionOverData((i, j) => result[i, j] = matrix[i, j] + matrix2[i, j]);
    return result;
  }

  public static Matrix operator -(Matrix matrix, Matrix matrix2)
  {
    return matrix + (matrix2 * -1);
  }
}

Answer 1

It was necessary to make an approximation by a polynomial of the m-th degree ... I
suspect the limitation of the accuracy of double ...
What could be the problem?

When solving such problems, it would be good to rely not on suspicions, but on mathematics - Runge Phenomenon . This topic is usually covered in universities as part of courses in computational mathematics (oh, what an absurdity is your higher education). Or you can at least google "high degree polynomial interpolation". The topic has been studied up and down for a hundred years.