How to implement curve recognition on canvas?

Question

Canvas

tell me how to do this and where to peep a ready-made algorithm or a ready-made library

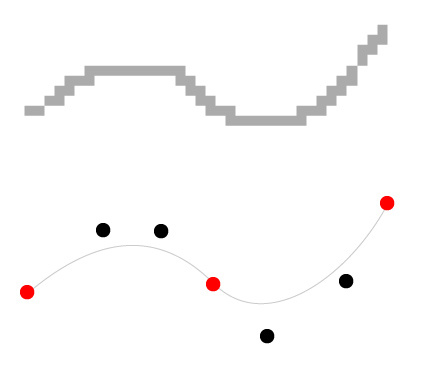
, first the user moves his finger along the canvas and as a result we get an array of points - this is the top picture,

you need to break it into fragments that can be described by cubic bezier curves,
that is, those that describe the curvature of a curve segment between two points on two points outside this curve

in this example, two fragments were obtained, the
start and end points are known
, the middle point and four points were initially calculated to describe the curvature:

Answer 1

paperjs.org/examples/path-simplification

Answer 2

I do not know ready-made solutions, but there are the following ideas.
First, let's learn how to approximate with a single curve. The first and fourth points are known to us - these are the first and last pixel. the coordinates of the other two anchor points of the Bezier curve are the four unknowns.
Compose the error function f(x1, y1, x2, y2) = (X(i/n)-x_i)^2+(Y(i/n)-y_i)^2. Here x_i, y_i - coordinates of the i-th pixel in the drawn curve, numbered from 0 to n, X(t), Y(t) - coordinates of a point on the Bezier curve - linear combinations of x1, x2 and y1, y2 with known calculated from t coefficients. This is actually the sum of the squared distances from each pixel to the unknown curve. It can be minimized like the least squares method - take the derivative over all variables, equate to 0. Get 4 unknowns and 4 linear equations. You can generally solve it on a piece of paper using the Krammer method, or you can calculate it using the Gauss algorithm.
There is an assumption here that the i-th pixel will be approximated by t=i/n points on the curve. Generally speaking, this is not guaranteed, but it will do as a rough measure of optimality. Maybe it will work just fine, I don't know. Experiment. But then you can honestly look for the closest point on the curve to a given pixel as the optimum of the 6th degree polynomial in t, when all the reference points of the curve are fixed. Here it is necessary to take the derivative, find its zeros and take the best t among them. To find the zeros of a polynomial of the 5th degree, you can recursively take the derivative, find the zeros of a polynomial of a lesser degree, and then, on each monotone segment, look for an intersection with OX binary search. Or use Newton's method. This is a problem that has been solved for a long time - there should be a lot of ready-made solutions.
When you have learned how to calculate the distance from a bunch of pixels to the Bezier curve, you can locally gradient descent along 4 coordinates x1, x2, y1, y2 to improve this correct metric from the optimum obtained by the rough metric.
So we can approximate a bunch of pixels of one curve. At the same time, we get a metric of how close the curve is to pixels. But you need to make it independent of length - so add the squares of the distances and divide by the number of pixels.
And then the algorithm is simple - eagerly bite off the longest pieces from your array of pixels, which are well approximated by the curve (give a small metric). To do this, you can stupidly sort out how many pixels we give to the first curve, count the metric and, if it is too bad, then stop. You can do something like a binary search here - increase the length of the piece by 2 times until the metric becomes bad, and then run the binary search, looking for the largest number of pixels that still gives a good metric. (here we use the assumption that the shorter the pixel curve, the easier it is to approximate).
This is an empirical algorithm and it is greedy in many places. There is no guarantee that it will give a mathematically optimal result, but there are many chances that it will give a reasonably good result.

Answer 3

If you need an algorithm, then read the description here .
If implementation then potrace.sourceforge.net

Answer 4

The first thing that came to mind was the search for the extrema of the curve. In this case, n consecutive extremum points are reference points. Further, I assume that the Bezier curve is described by a parametric equation and, having n reference points and a set of points on the curve, you can find the remaining reference points. Most likely, you need to solve a system of equations.
The trajectory itself is easy to calculate with a genetic algorithm. It is slow but easy to implement.