Answer the question
In order to leave comments, you need to log in
How to derive the polar equation of an ellipse, hyperbola, parabola?
here is the graph:
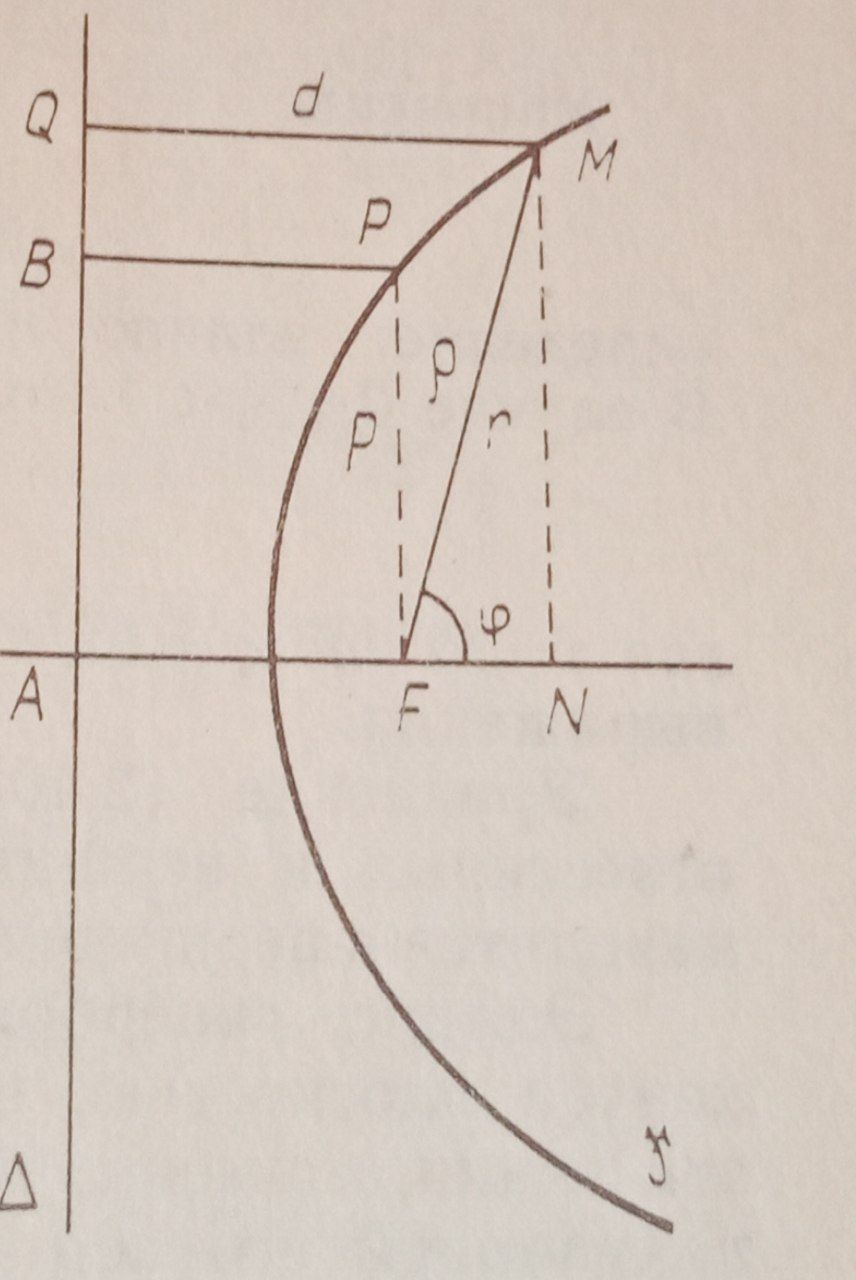
and here is the formula of this equation:
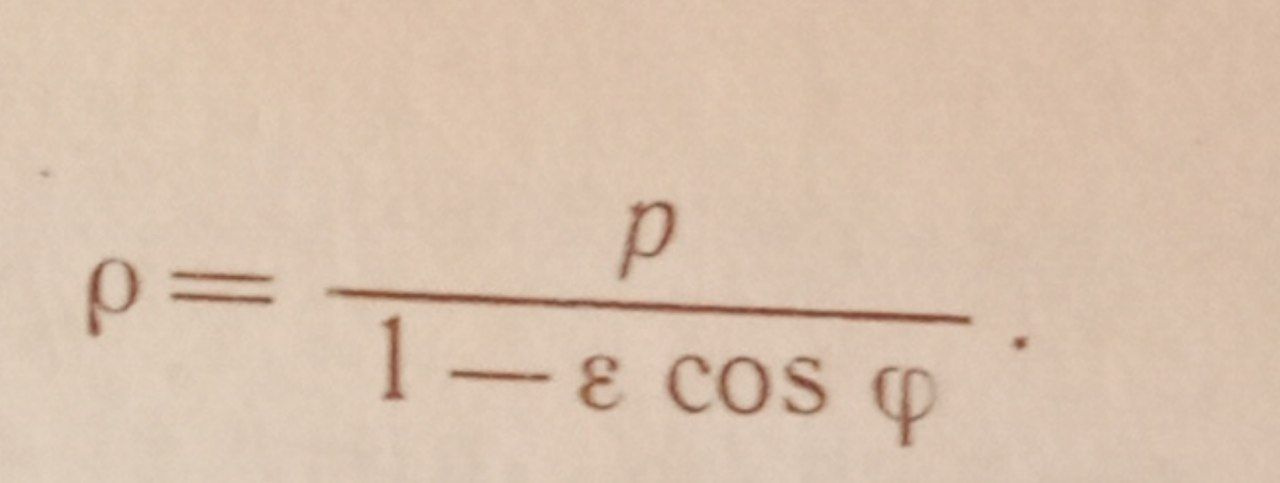
where p is the focal parameter equal to the axis b^2 / a. and (e) - Eccentricity. equal to the ratio of the focal length to the axis (a). How to derive this formula from a photo? according to the idea, the left side should be equal to Fn / cos f.
Answer the question
In order to leave comments, you need to log in
Google is not difficult:
publish.sutd.ru/e_books/analit_geometr_2014/glava/...
math.phys.msu.ru/data/24/lection_ellhyppar.pdf
Take the equation of your function as F(x,y)=0. Substitute x=x0+r*cos(fi), y=y0+r*sin(fi) there. Express r in terms of fi - that's the equation in polar coordinates.
There will be many formulas. First, the equation F(x,y)=0 must be written in terms of the exincessintret and the focal parameter. The focus coordinates must also be expressed in terms of them. Secondly, the expression with cosines and sines will have to be carefully combed using all sorts of trigonometric identities.
Didn't find what you were looking for?
Ask your questionAsk a Question
731 491 924 answers to any question