Answer the question
In order to leave comments, you need to log in
How to properly stop an object on collision?
Hello! I am studying the issue of object collision, I am writing a simple 2d engine for html5 for this. There are two convex polygons (in this case, rectangles), the coordinates are given by the center, the sides are vectors. In the picture below, the black rectangle is static, the blue one is moving towards it with a given velocity vector.
There is a collision detection algorithm, the intersection points are also known. Task: to correct the position of a moving object relative to a static one (simply stop), but the problem is that when the angle of the velocity vector changes, the required location changes after the adjustment (attached a picture). I still don’t quite understand in which direction to move in order to solve the problem that has arisen, I will be glad for any hint, thanks!
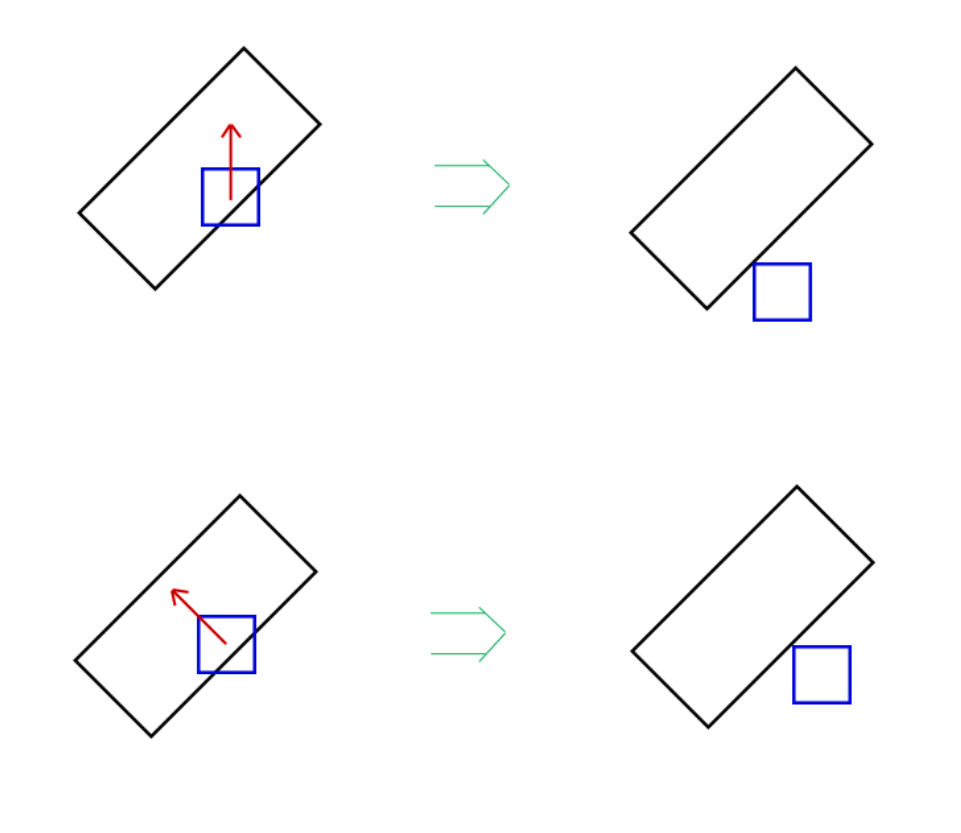
Answer the question
In order to leave comments, you need to log in
Your problem is that you allow an object to get into an obstacle and then don't know how to get it out.
At each iteration, you need to check the line segment along which your object is walking and look inside this segment for such a time parameter theta, at which the object begins to touch the wall.
After that, you just have to fix your object in this position.
The intersection search must be done analytically, it is faster.
Move along the normal of a static surface. In "adult" engines, you can't just move it, because it breaks all continuous physics, so instead of shifting, acceleration is added in the direction where you need to move it. This explains the jumping boxes and corpses and so on - due to calculation errors, objects constantly penetrate, shoot out and penetrate back when falling.
Firstly, if the speeds are small and the movement occurs in small segments per iteration, then you can push the object in any direction.
If the steps are not so small, then it is necessary, as Fox Jovovich already suggested , to shift to the intersection, and not to push the object into another and push it back.
There is a conceptually simple but far from the most effective method - binary search. Now you already know how to determine whether 2 objects intersect. Initially, they did not intersect, after shifting by 1.0 units of time they intersected. Do a binary search by time in the interval (0, 1): see if there is an intersection at a shift of 0.5 units of time. Then either 0.25 or 0.75 depending on the result of the check. And so on until the current segment in the binsearch becomes small enough. But this method has a big problem with high speeds - if during the iteration the objects pass through each other - you won't notice it.
A faster method is to actually look for the intersection of the trajectory. To do this, let rays from each vertex of one object parallel to its speed of movement relative to the second object. Then intersect each ray with the second polygon and find the shortest ray. Similarly, it is necessary to send rays from all the vertices of the second polygon in the opposite direction and intersect them all with the first polygon (this is if the moving person stumbles on the top of the obstacle sideways). We found the length of the minimum beam - move to it. If you set the rays parametrically in the form point+t*v, then in fact you are looking for the minimum value of the parameter t when crossing all rays (here v is the velocity vector for one time quantum, point is the coordinate vector of the point from which the ray was fired).
In this method, it is not even necessary to check whether the object hits an obstacle after a full step. We found the minimum distance to the intersection (maybe infinity if there are no intersections) - if it is greater than the shift per time quantum, then just move by the time quantum. in the parametric approach, this means that you are shifting by min(1.0, t).
This method can be optimized from quadratic to linear. Imagine that the motion vector is horizontal (and directed to the left). You can simply rotate all the points of each polygon along with the entire space, or use vector/dot products to determine which point is lower/left/right.
Find the lowest and highest point in each polygon. If these intervals do not intersect in OY, then the two objects will not collide, so you can stop checking. If the gaps on OY intersect, but the second object is located to the right of the first one, then they move away and again you can not check further. Here you can compare any one point from each object.
Then, as in the algorithm for merging two sorted arrays, take 2 pointers to the 2 lowest points in the objects. In the left object, the pointer will move counterclockwise, and in the right object, it will move clockwise. This way you will bypass the faces of the objects. See which of the two points below. Let a ray out of it and intersect with one segment - coming out of the current point on the second polygon up, and only with it. Move the pointer from the lowest point to the next one. Stop when you have reached both highest points.
This method is faster because you don't have to check intersections with all segments of the polygon near the ray, but only with one.
It is possible to optimize it to sublinear through binary search again, but here it is already very difficult. It is possible to search for the lowest and highest points for the logarithm using a bin search, and not, as above, by exhaustive enumeration of all points. Then, using a ternary search, iterate over the value of the Y coordinate and calculate the distance between the two polygons along this horizontal segment. To do this, again using a binsearch, find 2 segments intersecting this horizontal in both polygons and intersect with the horizontal to find 2 ends of the distance. This distance function dist(y) will be convex. Therefore, it is possible to find its minimum by ternary search.
Didn't find what you were looking for?
Ask your questionAsk a Question
731 491 924 answers to any question