How to construct a context-free grammar from the multigraph of a pushdown automaton?

Question

IT education

Greetings !
I study at the university, we are now going through context-free grammars. I figured out how to convert a context-free grammar into MP automata, but there were problems with how to find a context-free grammar if there is already an automaton.

There is the following MP-automaton (from the English PDA), this automaton admits the language L0 =L(M0)={a^ib^jc^k | i=j or j=k where i, j, k≥1}, which needs to be converted into a context-free grammar (from English CFG):


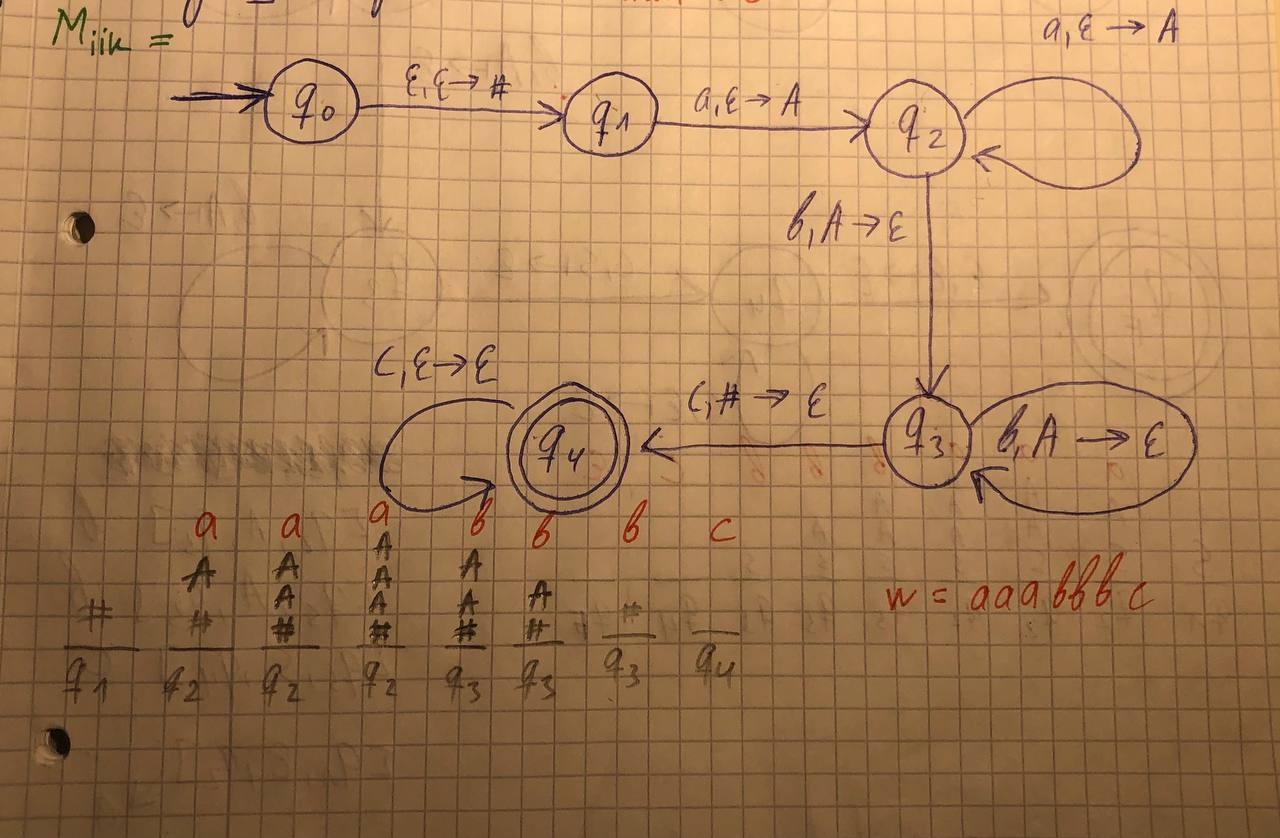
If I understand correctly, you first need to find the rules by which this automaton works and based on them build grammar. But with this, problems arose in this task.

I would be grateful for any advice!

PS I apologize in advance for a possibly not quite accurate presentation of the question or an error in terminology (I study in German, so I had to intuitively translate the essence of the task)

Answer 1

No, the reduced automaton accepts the language {a^ib^jc^k | i=j, i>=1, k>=1} - there can be as many letters c as you like, it has nothing to do with the number of letters b.
The first jump always puts # on the stack. Then, for each absorbed a of the original string, add A to the stack. Then b will be consumed along with A from the stack. Then swallow c from the string and # from the stack. Some c may be consumed at the end.
There is one way to build a grammar - first define the language, and then construct the grammar. I don't know of any automatic way.
First write a grammar for the language {a^ib^i, i>=1}. Then it can be easily converted to append c.
The grammar for such a language would be, for example:
S -> aSb
S -> e
To add c at the end:
Z->Zc
Z->S