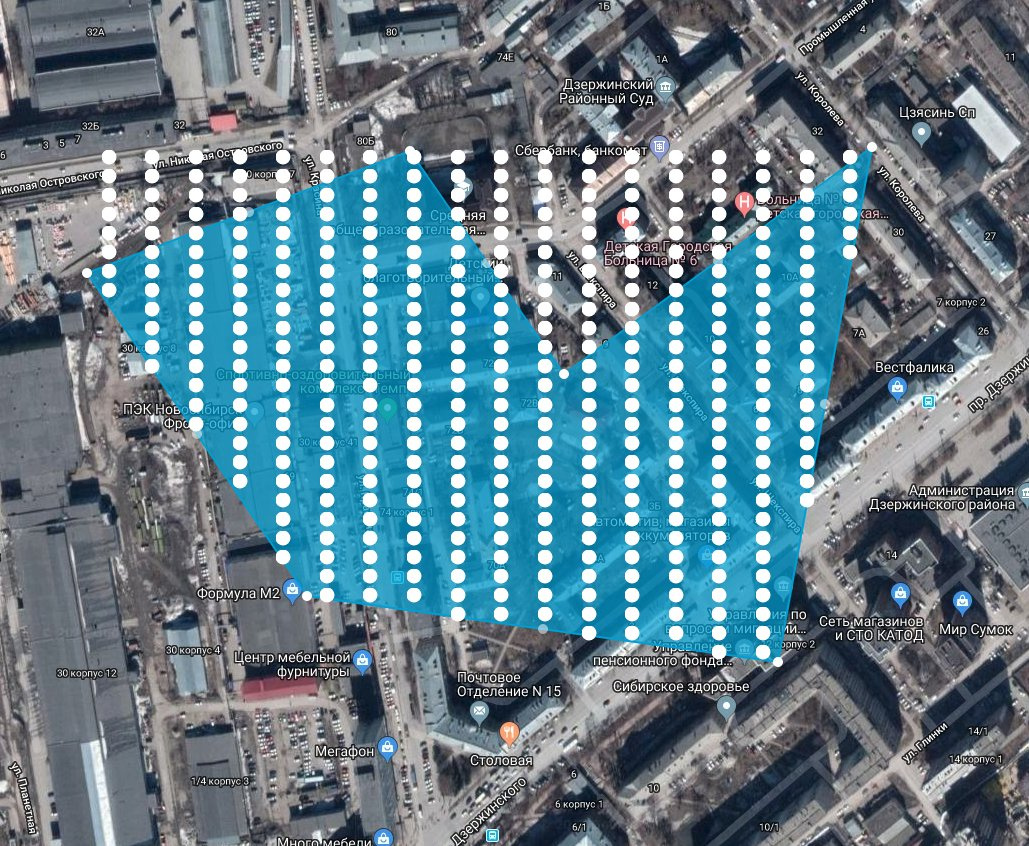
How to calculate the occurrence of points in a polygon?

Question

JavaScript

Colleagues, good day, in continuation of the earlier topic , I apparently encountered a lack of knowledge in geometry. The essence is this, I draw a polygon (leaflet) on the map, I get corners from it, I get the bbox of the polygon, and then I need to filter out the points from the bbox that are not included in the polygon, here is the actual code:
I get the bbox points:

return new Promise((resolve, reject) => {

            data.coords = [];

            let RECOMMEND_SIZE = 20; // шаг
            let BIAS_TO_CENTER = 0.5;

            let x_min = data.bounds.nw[0];
            let x_max = data.bounds.se[0];
            let y_min = data.bounds.nw[1];
            let y_max = data.bounds.se[1];

            let x_side_len = x_max - x_min;
            let y_side_len = y_max - y_min;

            let x_total_count = Math.round(data.width / RECOMMEND_SIZE);
            let y_total_count = Math.round(data.height / RECOMMEND_SIZE);

            let x_closest_size = x_side_len / x_total_count;
            let y_closest_size = y_side_len / y_total_count;

            for (let x = 0; x < x_total_count; x++) {

                for (let y = 0; y < y_total_count; y++) {

                    let coord_x = x_min + x_closest_size * (x + BIAS_TO_CENTER);
                    let coord_y = y_min + y_closest_size * (y + BIAS_TO_CENTER);

                    data.coords.push([coord_x, coord_y]);

                }

            }

            resolve(data);

        });

Next, I try to filter out the points (the code is taken from here ):

return new Promise((resolve, reject) => {

            data.polygonCoords = [];

            data.coords.forEach(item => {

                let x = item[0];
                let y = item[1];

                let xp = data.conners.x;
                let yp = data.conners.y;

                let xLength = xp.length;
                let j = xLength - 1;

                for (let i = 0; i < xLength; i++) {

                    if ((((yp[i]<=y) && (y<yp[j])) || ((yp[j]<=y) && (y<yp[i]))) && (x > (xp[j] - xp[i]) * (y - yp[i]) / (yp[j] - yp[i]) + xp[i])) {

                        data.polygonCoords.push([x,y]);

                    }

                    j = i;

                }

            });

            resolve(data);

        });

But in the end, I get the following picture:

Who faced the solution of such problems, I ask for help or advice! thank you in advance

Answer 1

The idea is the following.
1. Usually, a polygon, if it is not convex, is divided into convex ones (into triangles, in other words). Further, any polygon can be represented as the intersection of three or more half-planes (depending on how many sides your polygon has).
2. You can calculate the ratio of a point to a directed vector, i.e. on which side of the half-plane the point lies: on the left or on the right, taking into account the direction of the vector dividing the plane into two half-planes. Because A polygon is an intersection of half-planes, then you can determine whether a point falls into it by making sure that the point lies in all half-planes that form the polygon.
3. According to the above, we can write a function that determines that the point lies to the right of the vector that forms the half-plane. We will represent the faces of the polygon as vectors and we will go around the polygon in a clockwise direction, so "to the right of the vector" is always the half-plane that is "inside the polygon". After going through all the vector faces and making sure that the point lies "to the right" of them all, we conclude that the point lies inside the polygon.
4. The relation "to the right/to the left" is calculated by vector product (if it doesn't change me).