Euler project. Problem #15. How to decide correctly?

Question

Python

Guys, I started solving problems on the Euler project. I have already solved about 75 tasks, but there are a few tasks left that are not quite given to me on the way to finishing the first hundred tasks. I know mathematics and analysis quite well, but I didn’t study combinatorics, probability theory, or, moreover, anything related to such a search. There are two solutions here: use dynamic programming, or combinatorics. Brutus is real here, but it will take a very, very long time.
With my mind, I figured out that:
With N=20 (number of outcomes in one direction):
x = 2N! / (N! * N!)
x = 2*20! / (20! * 20!)
x = 137846528820 (correct answer)
But, again, I do not quite understand the mechanics of the search: the number of outcomes for any cell is a maximum of 40 options (20 down and 20 to the right), but how does the factorial help us here? And how can it be solved in another way? What formulas should be used, as well as what area of ​​\u200b\u200bmathematics, to find such solutions without dancing with a tambourine?
PS solved in Python
Starting in the top left corner of a 2×2 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner.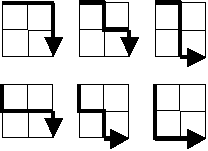

How many such routes are there through a 20×20 grid?
PSS Option in translation - euler.jakumo.org/problems/view/15.html
Thank you!

Answer 1

I understand that the question was asked 3 years ago, but I started solving Project Euler just now and maybe someone else will have questions about this problem. I will not write the code itself, read the comment from Vladimir Martyanov. To solve the problem "correctly" knowledge of algorithms is necessary. Here is a part of the theory (from 2:48 a recurrent case was found) https://www.youtube.com/watch?v=m4HOkVeN4Mo&list=P...
And another part of the theory is here (matrix construction) https://silvertests.ru /GuideView.aspx?id=34372
With this information, you should be able to write some pretty fast code yourself.

Answer 2

Factorials - because the number of paths are described by Pascal's triangle, and they can also be calculated through binomial coefficients. You can see the logic of the solution here

Answer 3

There is something wrong with the formula
x = 2N! / (N! * N!)
When N = 2 , the answer is 1
When N = 3 , the answer is (2*(1*2*3))/((1*2*3)*(1*2*3 )) \u003d 12/36 \u003d 1/3
How did you get a number greater than one with such a formula, if the denominator is always greater than the numerator

Answer 4

The number of steps in each possible path of 20 by 20 cells (21 by 21, since the steps occur between cells) from the upper left corner to the lower right will be 40. since we only have 2 step options - down and right, they can be denoted as 0 and 1.
In fact, this is the number of possible combinations for a length of 40 characters, consisting strictly equally of 20 ones and 20 zeros. For example, for 2 by 2 (3 by 3) the path length is 6 steps, for 4 by 4 (5 by 5) - 8. for 20 by 20 (21 by 21) - 40. And everything would be fine, but itertools takes the system into knockout counting all possible sequences of 0's and 1's of length 40...