Algorithm for arranging circles on a rectangular area with obstacles

Question

JavaScript

It is necessary to place the signal sources (circles) on a rectangular plane in which rectilinear obstacles are specified. Questions:
1) What algorithms are suitable?
2) What options exist (more or less optimal algorithms, enumeration)?
3) Will JavaScript pull such calculations?
Thanks in advance for the answers, I will be glad to answer even one of the above points! :)
UPD. Some clarifications that I myself recently learned: the specific goal is to cover the entire room with a signal, while optimally and prevent sources from crossing in the near zone; the range of each source can be set to be infinite.

Answer 1

In this (refined) formulation, the problem is interesting and nontrivial.
Let me suggest some coarsening, which, in my opinion, based on the subject area, will not greatly distance the suboptimal solution from the optimal one, but will allow us to move away from geometry to discrete mathematics:
Let's introduce Cartesian coordinates in the indicated room so that the obstacles are strictly along the boundaries of single cells.
Let's add the following assumptions/restrictions:
a) we place signal sources only in the centers of the cells,
b) we consider that in each of the four diagonal directions the signal is not visible in the cells located behind the corner (corners) of any obstacle (see Fig.)
c) in four direct directions, the signal is obviously not visible behind the first obstacle and also nowhere further than this coordinate (see figure).
As a result, for each cell as a potential signal location, it is possible to determine a Boolean cell availability matrix.
In general, the problem is reduced to finding the minimum set of such selected matrices (corresponding to the source location cells) that would provide complete coverage of the room.
It seems to me that for large matrix sizes, this is effectively implemented only by heuristic search algorithms (I am a supporter of genetic algorithms, but of course there are other approaches).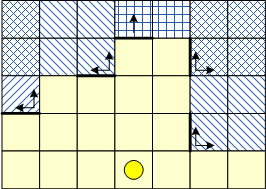

Answer 2

It looks like this to me:

1. The plane with obstacles is divided into rectangles (it is also worth choosing an algorithm here)

2. http://ru.wikipedia.org/wiki/Packaging_balls

I won’t say anything about JS performance, it depends on the number of balls and the selected algorithms.

Answer 3

Every arrangement has a purpose. What is yours?
Cover all space with a signal?
Or vice versa to prevent the signals from crossing at the point ?
Are the diameters of the circles equal?
By what criterion do we optimize?
The task is still unclear.