Answer the question
In order to leave comments, you need to log in
Why is there a significant difference in the calculation time in solutions with the same complexity?
Hello!
Recently I came across a fairly simple problem: given an array of integers and the number "a", you need to find the first number closest to "a" in the array.
Not the most optimal option immediately came to mind - to calculate the module of the difference with a for all numbers in the array, find the minimum and stop in the third pass if it matches.
Then I realized that the problem can be solved in at least 3 more ways (via key in min, via reduce, via a simple self-written algorithm) and decided to measure the calculation time for each method.
def time_deco(func):
@wraps(func)
def wrapper(*args, **kwargs):
start = datetime.now()
res = func(*args, **kwargs)
return (datetime.now() - start).total_seconds()
return wrapper
@time_deco
def with_min(a, l):
return min(l, key=lambda x: abs(a-x))
@time_deco
def with_reduce(a, l):
return reduce(lambda x, y: x if abs(a-y) >= abs(a - x) else y, l)
@time_deco
def with_map(a, l):
z = min(map(lambda x: abs(a-x), l))
for i in l:
if abs(a-i) == z:
return i
@time_deco
def traditional_way(a, l):
value = l[0]
i = abs(a - value)
for item in l:
if abs(a - item) < i:
i = abs(a - item)
value = item
return value
my_funcs = [with_min, with_reduce, with_map, traditional_way]
a = random.randint(0, 500000000)
random_list_100 = [random.randint(0, 100) for _ in xrange(100)]
random_list_100k = [random.randint(0, 100000) for _ in xrange(100000)]
random_list_1kk = [random.randint(0, 1000000) for _ in xrange(1000000)]
random_list_100kk = [random.randint(0, 100000000) for _ in xrange(100000000)]
random_list_200kk = [random.randint(0, 200000000) for _ in xrange(200000000)]
random_list_300kk = [random.randint(0, 300000000) for _ in xrange(300000000)]
for_df = dict()
for func in my_funcs:
for_df[func.__name__] = [func(a, random_list_100),
func(a, random_list_100k),
func(a, random_list_1kk),
func(a, random_list_100kk),
func(a, random_list_200kk),
func(a, random_list_300kk),
]
df = pd.DataFrame(data=for_df)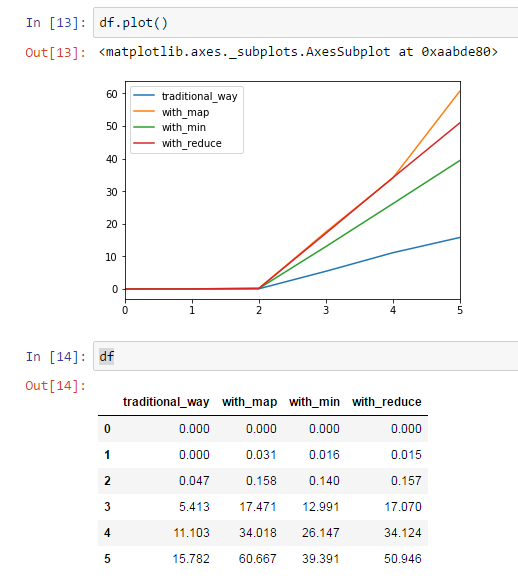
Answer the question
In order to leave comments, you need to log in
Blame the overhead.
In traditional_way they are minimal.
Replace lambdas by calculating an intermediate array containing abs(ax) in other cases and get an additional performance boost.
Why is there a significant difference in the calculation time in solutions with the same complexity?
"I won't tell you for the whole of Odessa" :-), but let's compare only with_map(a, l) and traditional_way(a, l). Both functions have a loop (for item in l:) that runs in about the same time. But with_map also contains the line
z = min(map(lambda x: abs(ax), l)) , which first performs map(lambda x: abs(ax), l) -
another pass through the array, and in the resulting looks for min - i.e. runs through the list again. Total - three passes through the array, instead of one in the traditional_way. With other functions - about the same story. (For example, min(l, key=lambda x: abs(ax)) is at least two passes through your list).
Didn't find what you were looking for?
Ask your questionAsk a Question
731 491 924 answers to any question