Why is the child calculated in the d-ary heap by such a formula?

Question

Data Structures

We have a heap with the number of children per node equal to d. We number all elements in it from 1 to n, where n is the number of all nodes. we will number the nodes in turn in each level, so that it turns out something like this:


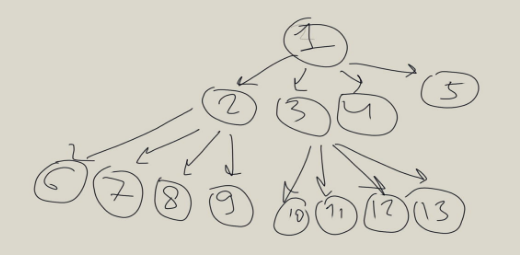
I found out that the formula for calculating all children in such a tree is:
{(i−1)d+2,…,min{n,(i−1)d+ d+1}}
Can anyone explain, or at least point me in the right direction, why this formula works? How was it formed? (here min for the case when the tree is out of bounds)

Answer 1

It is more convenient if you number the vertices from 0. Then the children will be d*i+1...d*i+d. Your formula is obtained from this by simple renumbering (subtracting and adding one in the right places). Next, I will talk about this formula.
In this formula, it is obvious that the father of node k (with number > 0) will be floor((k-1)/d). Further, it is clear that for two different vertices, the numbers of their children will not intersect in any way (because these are segments of d numbers shifted at least d relative to each other). You can also prove by induction that all numbers from 1 to infinity will correspond to some vertex in the tree (we can get the father by the formula (x-1) / d, by induction he is already in the tree, and hence the current number corresponds to the top).
Intuitively, multiplication by d appears because at each next level of vertices there are exactly d times more than at the previous one. All children of one vertex go in a row, so they will be in the formula +1, +2 ... for children.