Which regression algorithm to choose for noisy (scattered) data?

Question

Machine learning

I want to build a regression with multiple variables (multiple features). In my data, I have n = 23 variables and m = 13000 training examples. Here is a graph of my training data (apartment size vs price):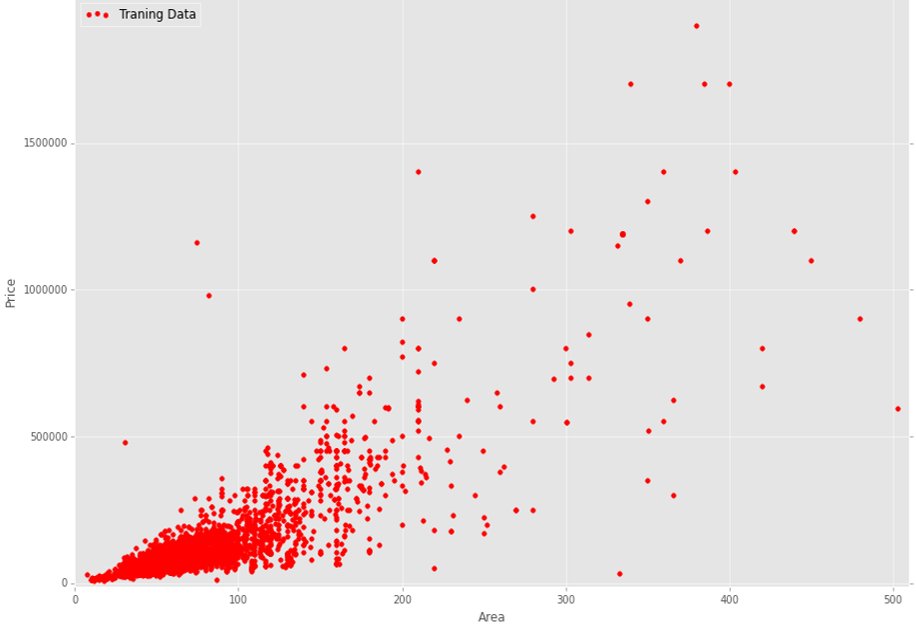

13,000 training data are plotted here. As you can see, this is quite noisy data. My question is which regression algorithm is more suitable and reasonable to use in my case. I mean is it logical to use a simple linear regression or is it better to use some non-linear regression algorithm.
For clarity, I will give examples. Here is an abstract example of linear regression: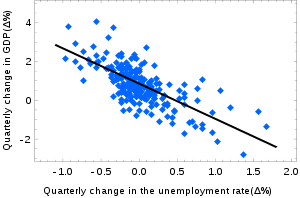

And also an abstract example of non-linear regression: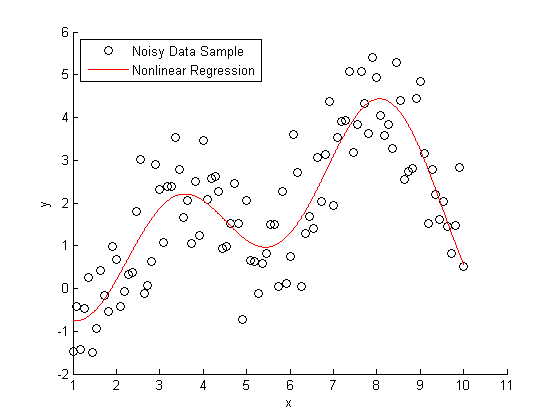
And here are examples with hypothetical regression lines for my data: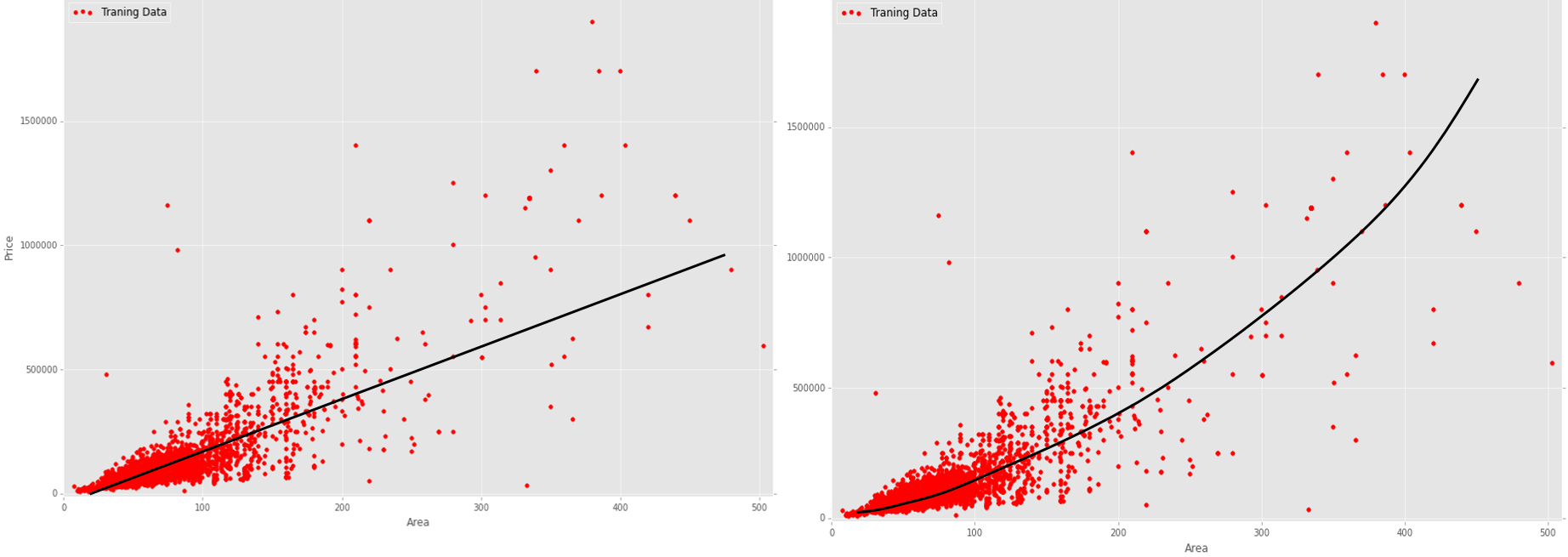
As far as I understand, primitive linear regression for my data will produce a large total error (error cost), since this data is noisy and scattered. On the other hand, there is also no distinct non-linear dependence (for example, sinusoidal) here. Which regression algorithm is more rational to use in my case (prices for apartments) in order to get a more accurate price prediction. And why is this algorithm (linear or non-linear) more rational?
Addendum:
This is how my graph of the linear dependence of the price on all 23 parameters looks like, displayed on the price-area data: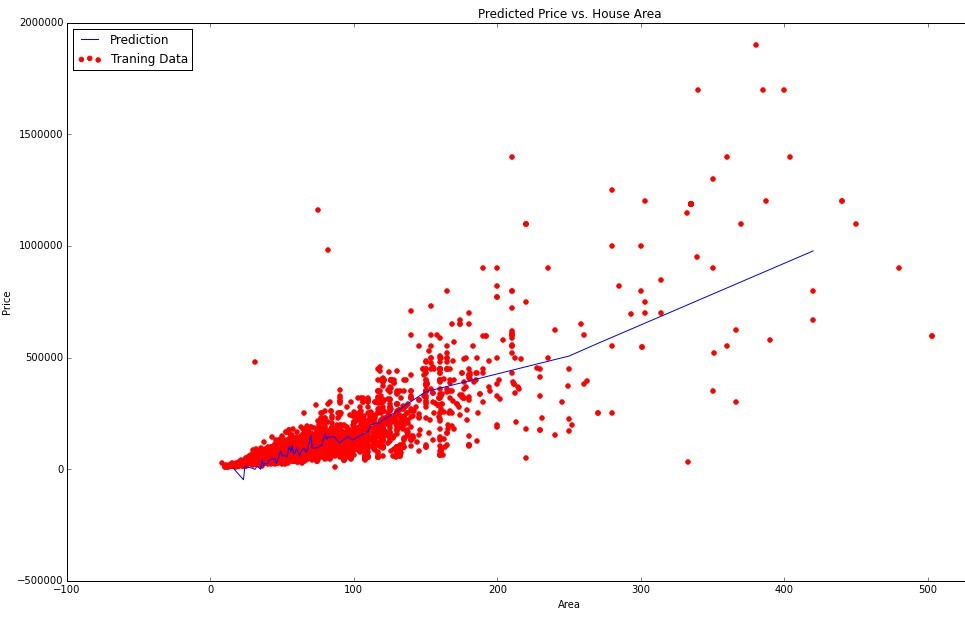

I don't know what the NON-linear dependence would look like in this case. And it would be more rational than linear.

Answer 1

and you make an equation like y=t; t= sum(k1*x1^2+k2*x1+k3)

Answer 2

what the hell is on the graph all the parameters are mixed?
it is quite obvious that each parameter contributes to the model with a certain weight, you need to choose weights for these parameters.
start with a linear relationship, then you can go to polynomials of the 2nd or 3rd order if you really can't wait.
you can estimate the total error (cost) everywhere, which model with a smaller error, this type is better.

Answer 3

take the average of each vertical unit.
then you can try to change the step in order to see the overall trend.