What mathematical expectation will be correct?

Question

Mathematics

So I have a random variable, each value of which can be found using the equation:
X = an^2+bn+c
n belongs to natural numbers.
I have a probability for each number:
P = p*q^(n-1)
q = 1 - p
What is the correct way to find the mean?
Like this:

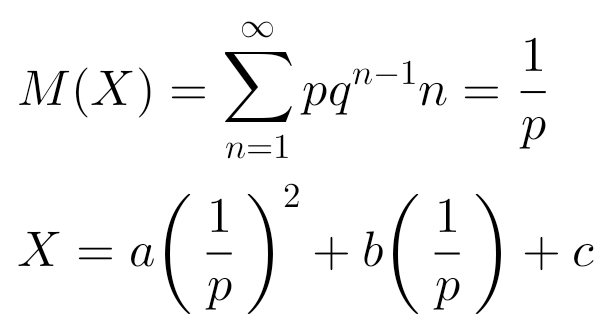
Or like this:

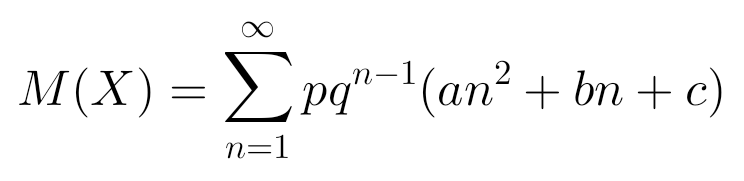
Simply, the point is that I can find the average number and use it to find the value of X, will it be average?
Or calculate the mathematical expectation using the value of X as a random one.

Answer 1

I can find the middle number and use it to find the value of X, will it be the average?

In no case!
Let me formulate a rule:
Let me have some random variable R. And there is a function T(R).
If the function T(R) is linear, i.e. T(R)=a*R+b (where a and b are constants), then in this case M(T(R))=T(M(R)) ; those. here you can first average the argument of the function, then take the function from the average value of the argument.
If the function T(R) is non-linear and its second derivative is positive, then M(T(R))>T(M(R)) .
For example, consider T(R)=R ^{^2} and R symmetrically around zero. You can even take R, which is equally likely to be distributed between the values ​​"one" and "minus one", it's quite simple. Due to symmetry, M(R)=0, but M(T(R)) will obviously be greater than zero.

Answer 2

Answer 3

Not right. It is necessary to sum the product of the values ​​​​and their probabilities. You stupidly multiply n by probabilities, but you need X (n).
But you also calculated the sum of the series incorrectly. And you have to count something like that. There you can derive a formula through the integration / differentiation of series.