Answer the question
In order to leave comments, you need to log in
What is the algorithm for seating players on several tables with the conditions in the description?
There are 25 teams of 4 people each. Players on the same team should not sit at the same table.
There are 10 tables, each seating 10 players.
Each player must play 10 games, and it is desirable that the players play approximately the same number of games with each other (if possible). It is desirable that each player plays at least once with other players (except members of his own team).
There is an old seating on the screen, but it is lousy - a large number of players do not play with each other at all.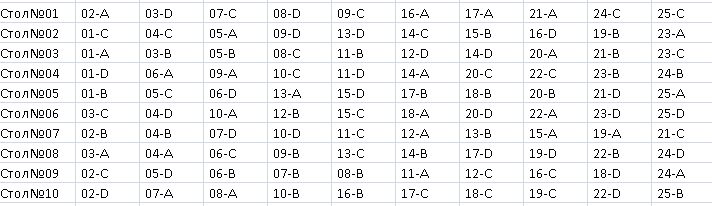
Answer the question
In order to leave comments, you need to log in
The minimum task is a one-time solution to the problem.
Ideal - the ability to create more and more new seating arrangements for a different number of players and tables. The method of creating seating arrangements is very interesting, I have no idea how to solve this problem correctly, if not randomly form an array, checking whether it fits the restrictions :)
Didn't find what you were looking for?
Ask your questionAsk a Question
731 491 924 answers to any question