What architecture to choose for a neural network that solves the problem of matrix transformation?

Question

Neural networks

Hello!
There are 10 thousand pairs of matrices (input and output) 100 * 100 on hand, and the input can be converted into an output by applying a certain law that is unknown to me.
The input matrices contain fractional values ​​of a wide range: from zero to several thousand (95% - zeros), and the output matrices contain integer values ​​(95% - zeros), reflecting belonging to one of the 16 classes.
In addition, there are 1000 input matrices 100 * 100, for which you need to more or less accurately reproduce the output.
The first thought that came to my mind is that I have a regression task, which means neural networks should help. Because Since the input and output matrices have the same dimension, it makes sense to use the architecture of the form U-Net/DeconvNet/SegNet/RedNet/FCN. The choice fell on RedNet: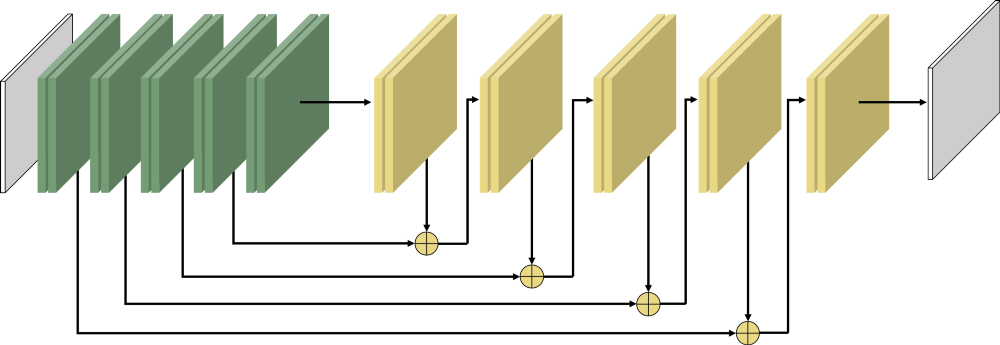

If I use the activation function of the last Sigmoid layer, then after training on 2.5k samples, I get an accuracy of about 0.5 and a complete mess in the output. If the activation function is ReLu, then the accuracy is 0.9, but only zeros are correctly detected in the output, and the rest of the values ​​\u200b\u200bgo beyond a thousand.
Previously, it was possible to train only U-Net in the problem of segmentation into "there is a road" and "there is no road".
Whether I was mistaken with a choice of architecture?
If not, then I think I made a mistake in how I train the neural network: you need to split the output matrix into 16 mask matrices, which would contain information about the presence of only a specific class in a given cell of the matrix. Those. as it is done in U-Net when segmentation into several classes is carried out. Well, the activation function of the last layer will be SoftMax, and there will be 16 output masks. Is my guess correct?

Answer 1

I correctly understood that you need to classify each cell of the 100x100 matrix, the structure and rules of formation of which you do not know, into one of 16 classes?
What is the nature of the data? It may well be that convolutional layers are not relevant here.
In general, you need an output layer with 16-dimensional Softmax per pixel (it turns out a batch * 100 * 100 * 16 dimension tensor), then you take argmax + 1 for each pixel, and use cross-entropy as a loss function.
UPD: it dawned on me that during training it is better not to take argmax, but instead apply One-Hot-Encoding to the class matrix in order to get a tensor of the same dimension as the predictive one.
argmax is useful at the post-processing stage, when the network is already trained and gives the correct probabilities for the classes.