What algorithm should be used to obtain the coordinates of a section by a plane of a polyhedron?

Question

Mathematics

Colleagues, good afternoon!
In its original form, the problem can be described as follows, there are many relatively simple polyhedra (about 300-500 pieces). There is a cutting plane. It is necessary to obtain a section of all these polyhedra. The task can be simplified to finding a section of one (each) polyhedron - the final section will be the sum of all sections.
Each polyhedron is defined by two opposite faces and is stored as a list of pairs of points - a point on the first face and its corresponding point on the opposite face. In other words, for every point on a face, there is always a pair on the opposite face. In the figure below, such pairs of points are A1 - A2, B1 - B2, etc. But there are also polyhedra whose faces are not convex figures (as in the figure).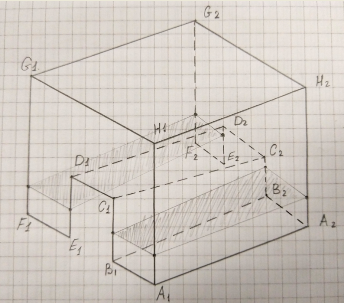

And for such polyhedra, the current algorithm builds an incorrect section. The essence of the current algorithm is to go through each face, find the intersection points of the edges of the face by the cutting plane (if the face is a convex polygon, we get a maximum of 2 intersection points), connect these points, connect the segments of the sections of adjacent faces, and get the final section. If the face is not a convex polygon, then I can’t figure out how to get a section of this face, what points to connect?
Tell me where to dig or how to modify the existing algorithm so that it works with "problematic" polyhedra or in other words, how to cut edges that are not convex polygons?
Thank you.

Answer 1

Dig here:

• Boolean operations on polytopes and pologins
  
• Binary Trees for Solving Boolean Operations
  
• The intersection of a straight line and a slope
  

Answer 2

Mmm, far from the queen of all sciences, three ideas, the next one is better than the previous one.
Check the figure for convexity, if it is not, complete it to be convex. Calculate the section of the new figure and subtract from the resulting section what was completed. Pitfall - what you completed may not be a convex figure.
Option two, check the figures for convexity, if it is not, break the figure into separate convex figures.
Option three, forget about checks and split each section into a guaranteed convex polygon (triangle). Well, or the figure itself into triangular pyramids. And already consider the sum of the sections of these triangles / triangular pyramids.
But these are thoughts. I think there is a more beautiful solution based on some theorem. According to the subject, I only remember that a figure is convex if the segment connecting any two points of this figure lies inside this figure.
Maybe if you store the figure as a set of vectors, the problem can be solved more easily through the methods of vector algebra. But I can’t say more precisely, since I was a dunce and in pairs while studying at the university I did anything but study itself.