What algorithm is suitable for describing the flight of an insect?

Question

Algorithms

The essence of the problem. I am writing an IOS Sprite Kit game. It is necessary to realize the chaotic flight of the insect. Now it turned out like this: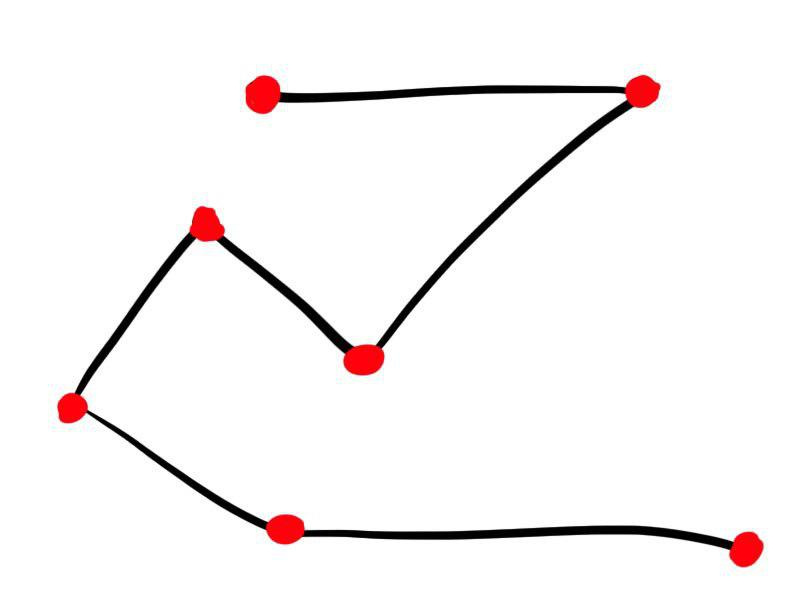

This is not like the flight of an insect . It is
necessary that the flight path be something like this:

I understand that it is necessary to build curves through arbitrary points, but I just can’t figure out how to correctly define random points so that I can build a normal curve. Plus, what about turns? You also need to control that the insect does not leave the screen borders. Several fly at the same time. And the saddest thing is that the insect is not an abstract point, but it has clear outlines, i.e. the head should point in the direction of travel. The sprite will constantly need to be rotated. Tell me which way to dig? Maybe in swift there are some other solutions to similar problems? Maybe there is another way to solve it? While looking at the Bezier curve, and somehow I can’t adapt it to this task. In general, I will be glad to any advice.

Answer 1

You can make a pursuit chain : one is drawn to a random point, another is drawn to it, etc., and the last one is a fly.
Put another point on the plane randomly, anywhere within the allowable area. This point is the target that the next, invisible point tends to: each next frame, its coordinates change to k * векторИзТекущегоПоложения-в-Цель:

x = x + k * (xTarget - x);
y = y + k * (yTarget - y);

So the "pursuer" slows down as it approaches the target, never reaching it.
This invisible point is not alone. The next one strives for it, as for the goal. One more to that one. Finally, the fly itself, according to this law, tends to the tail of this chain - the next point.
The more links in such a chain, the smoother the curve. When the fly approaches the target closer than D, the next random target is generated.
Made a working example .
You can change the algorithm and make, say, the linear speed constant. Or randomly vary the parameters k and D - this will change the speed and trajectory from a smooth closer to a broken line.

Answer 2

There are at least a dozen flight types . Which one do you need?

Answer 3

those. head should point in the direction of travel

The direction of movement will be vector = tangent to the curve at the given point * (velocity vector / velocity value)
mathserfer.com/theory/kiselev2/node64.html
Here is how to find it.
The derivative at a point is programmatically calculated through the definition of the derivative of the ratio of the difference of values, see the definition of the partial derivative through the limit and how to find the total derivative through it.
In order for the trajectory to be smooth, more points must be generated. To have arcs - use trigonometric functions.
The main rule that will help:
* need cyclicity - cos/sin etc
* need smoothing between some boundaries - sigmoid
* need growth - higher order functions
In this case - we need a 2d function that will take x, y and return z, a similar picture will be its projection onto the 2d-plane
Take the function:
f(x(t1), y(t1)) = a*cos(x(t1))^k + b * sin(y(t1))^t + O, where a ,b,k,t, O - variables that you randomly select to give a unique look, t1 - time, f(x(t1),y(t1)) - fly z height, depending on its x,y coordinates
I don’t know how to give a practical example, so I will give in python, some hypothetical drunken fly or a mosquito stoned by a raptor

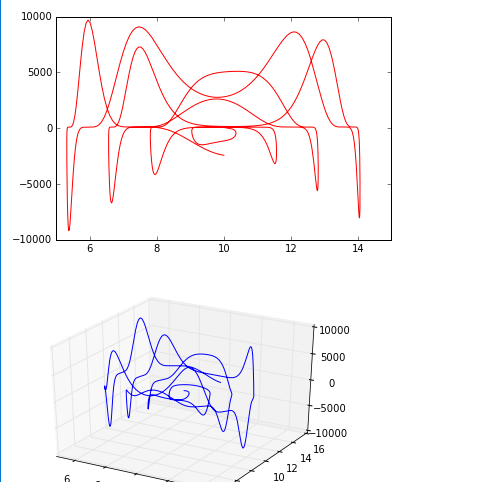
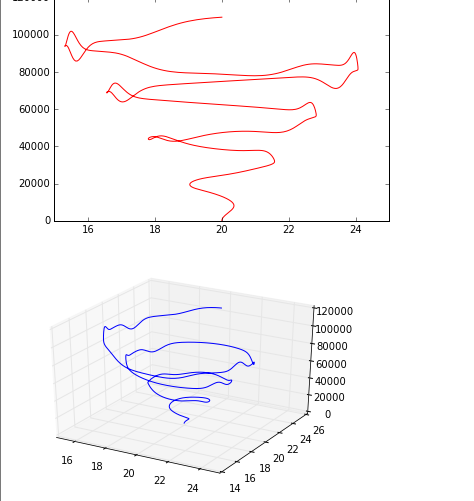
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
def func(x, y, a, b, t, k, O):
    return a * np.power(np.sin(x), t) + b * np.power(np.cos(y), k) + O

t = 5
k = 5

theta = np.linspace(-4 * np.pi, 4 * np.pi, 1000)
time = np.linspace(0, 5, num=1000)

a = 10
b = 10

x = time * np.sin(theta) + a
y = time * np.cos(theta) + b

z = np.asarray([func(x[i], y[i], a, b * i, t, k, 100) for i in range(len(x))])


plt.plot(x, z, 'r')
plt.show()

fig = plt.figure()
ax = fig.gca(projection='3d')


ax.plot(x, y, z)

In short, the vector in which direction to move is clear. Stupidly iterate over the generation functions x, y and z until you find the right beauty

Answer 4

I remembered that I forgot to unsubscribe on solving this problem.
I solved it in SWIFT as follows. We build the N-th number of points, we build a spline through these points. We move the object using SKAction.follow, it allows you to set the orientation in the direction of movement, after completion we build new points. Smoother movement can be achieved by generating points without sharp deviations from the current direction of movement, so that the object does not abruptly change direction in the opposite direction. Thank you all for your help

func Yellow()
    {
        var object = self.childNode(withName: "//yellow") as! SKSpriteNode
        yellowMove(object: object)
    }

    func yellowMove(object obj: SKSpriteNode)
    {
         var chain = [CGPoint]()
        chain.append(CGPoint(x:obj.position.x,y:obj.position.y))
       // генерируем 6 случайных точек.
        for var i in (1..<6) {
            chain.append(CGPoint(x:getRndX(),y:getRndY()))
        }
         // Строим сплайн через эти точки
        let ground = SKShapeNode(splinePoints: &chain,count: chain.count)
        let anim=SKAction.follow(ground.path!, asOffset: false, orientToPath: true, duration: 10)
        // по завершении перемещения, опять запускаем функцию
        obj.run(anim,completion:{
            self.yellowMove(object: obj)
        })
    }

Answer 5

In addition to splines, there are many other types of shapes. The simplest option is to set the destination randomly and for smooth movement use the formula newpos=K*pos+(1-K)posz, where pos is the current position in vector form, posz is the given position. The more K, the smoother the curves will be, but without casting. You can complicate for beauty, but then you have to understand the diffusers.

Answer 6

And in my opinion it is much better to make a dozen predefined trajectory maps, with transition points from one trajectory to another.
Pure random is a rather evil thing, because it is uncontrollable.

Answer 7

The task is very similar to the node smoothing algorithm. I think the easiest thing you can do is write to the developers of Inkscape (an open vector editor), and ask them where to dig to implement such a feature (if you take their code, the game will have to be published under the GPL), for fun, download Inkscape, stumble directly with arbitrary number of nodes, and then flatten them. You will be surprised how straight sticks turn into graceful curves, and the curvature can be adjusted with "levers" (that is, there are variables in the code responsible for this). There is also a Spiro curve. It is more suitable for your task than Bezier. Here is a straight line without

smoothing

She with smoothed

dots

Answer 8

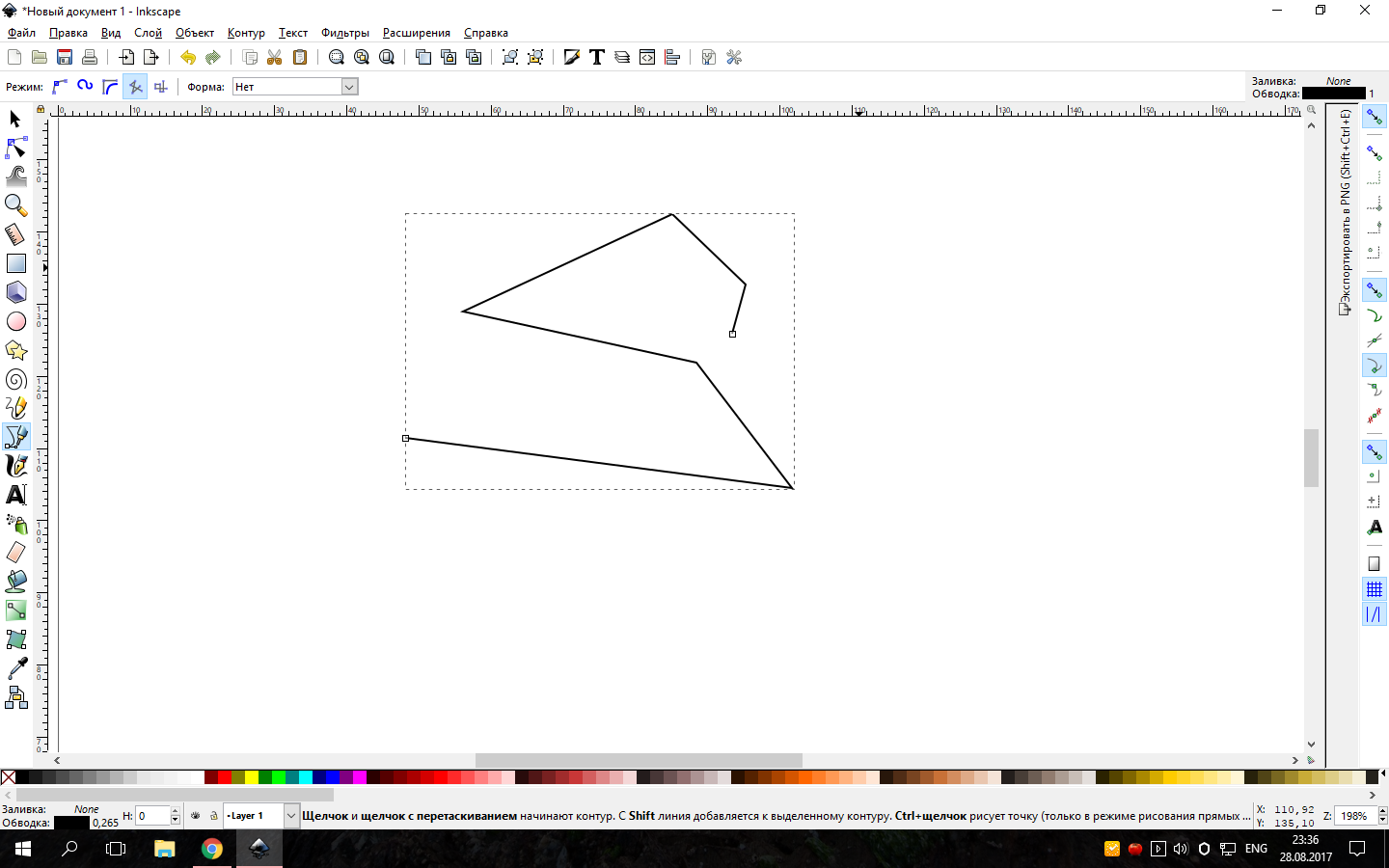
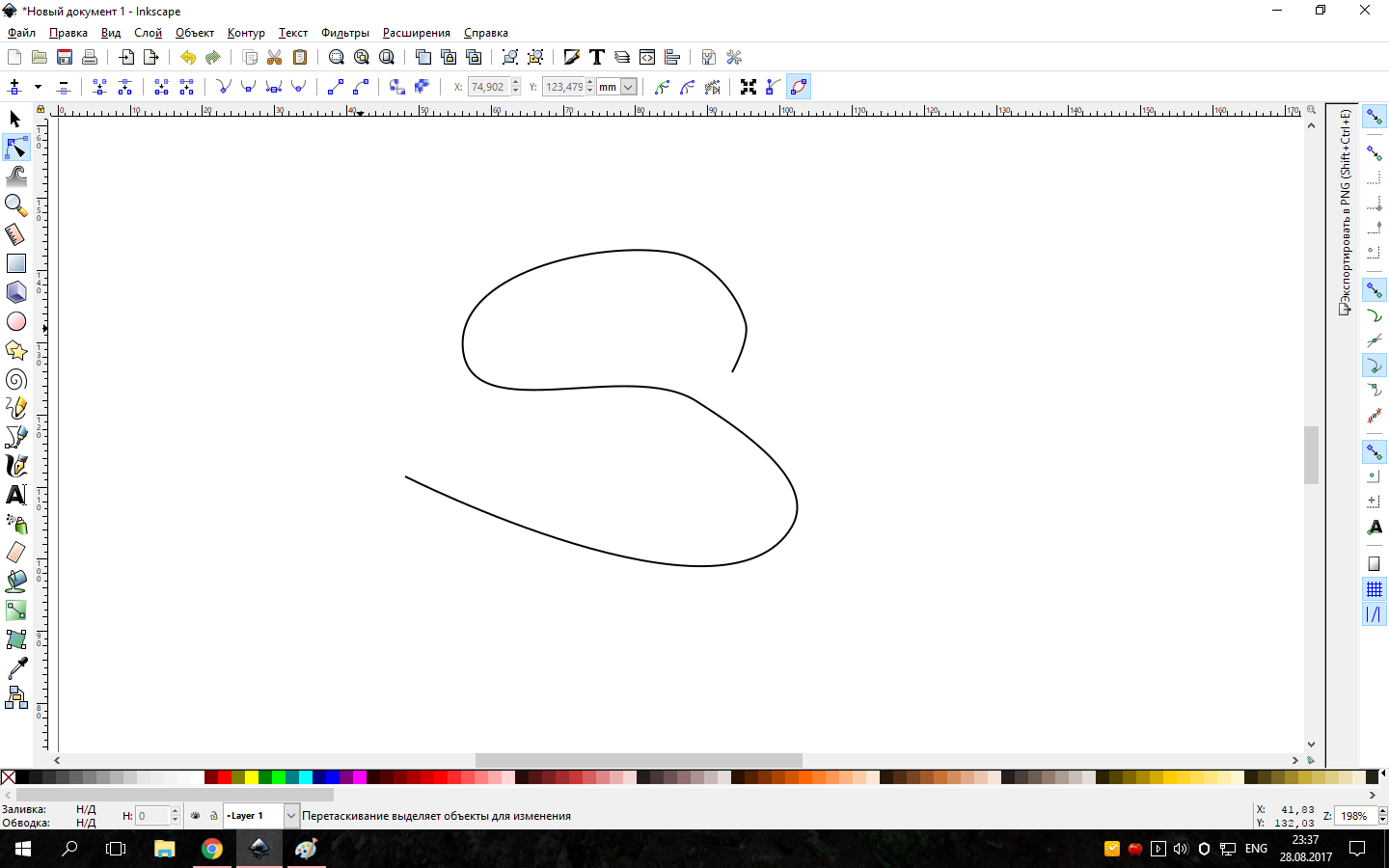
Restrictions on the speed of the angle of rotation (the head of the sprite is always directed along the velocity vector).