How to cover a polygon with lines?

Question

Programming

Good afternoon!
There is the following task:
The program displays an area (by coordinates), that is, its boundary points are given, and it can be drawn, it looks something like this: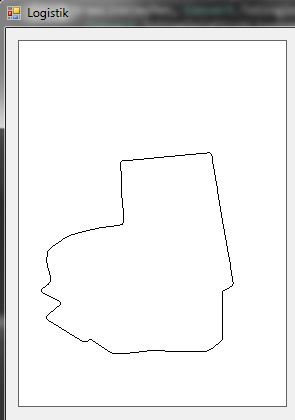

This area needs to be covered with lines like this, for example: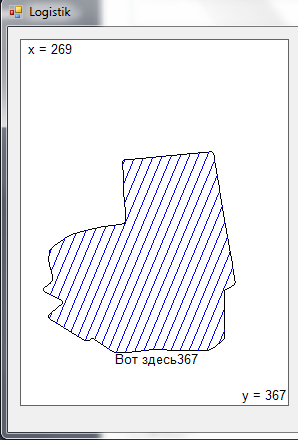

These lines intersect the area at some points, and outside the area are not drawn.
Next, you need to rotate these lines, and count how many times the lines intersect with the area, and so on several times, and from all options choose the coverage with the minimum number of intersections.
I can't implement rotation, writing huge crutches... :(
HELP)
Working in Windows Forms, C#. I will be glad for any help!

Answer 1

I propose to rotate not straight lines, but a figure. To do this, it is enough to multiply the coordinates of each vertex by the rotation matrix. Well, straight lines can be taken horizontal (y=c1, y=c2, ...). This will make it much easier to find the intersections of the sides with these lines.

Answer 2

Equation of a straight line y=kx+b. K is responsible for the turn. k=tg A, where A is the elevation angle.

Answer 3

As an alternative - draw lines by BoundingBox and clip them with Clipping:
https://docs.microsoft.com/en-us/dotnet/framework/...

Answer 4

Why draw straight lines? Paint with a brush.

Answer 5

Не нужно рисовать сразу все прямые.
Нужно найти на указанном контуре две точки, наиболее удаленные друг от друга.
Далее рисовать линии разметки перпендикулярно линии проведенной через найденные выше две точки.
Так как точки наиболее удаленные (условно самая длинная хорда), количество линий разметки будет максимальным.
Для поиска наиболее удаленных точек, можно по координатам точек образующих контур вычислить геометрический центр масс фигуры и затем найти точки контура наиболее удаленные от нет по формуле Евклида.
Далее для каждой найденной точки строим луч из текущей точки через геометрический центр масс и ищем точку пересечения этого луча с контуром.
Исходная точка контура и найденная путем трассировки луча образуют отрезок, нужно найти и запомнить длину отрезка.
После этого имеем массив отрезков с длина, нужно выбрать самый длинный (или один из самых длинных, если есть несколько равных по длине).
Найденный отрезок и будет проходить через наиболее удаленные точки контура и перпендикулярно ему нужно строить линии разметки.

Answer 6

Два параметра можно варьировать: угол решетки и её фазу, смещение линий параллельно самим себе в рамках одного шага решётки.
При относительно сложной форме фигуры остаётся только перебор вариантов. Сначала с большим шагом, затем уменьшая шаг и уточняя.
Не совсем понятно, как задана фигура?
«даны точки границ ее» – это массив точек с небольшим шагом, т.е. контур задан пунктиром, или «углы» прямых отрезков (вся фигура составлена из множества прямых отрезков разной длины).
Алгоритм примерно такой. Пара (угол, фаза) задаёт множество прямых. Надо пройтись по контуру фигуры, считая пересечения или близость очередной точки контура к одной из прямых. Если контур задан прямыми отрезками ещё проще: для каждого отрезка посчитать число пересечений, исходя только из расстояния краевых точек от одной master-прямой. Например, расстояния 5.2 и 7.3 при шаге решетки 3. 0 не пересекает, 3 пересекает, 6 пересекает, 9 уже нет. Итого 2 пересечения.
Прямая задаётся уравнением Ax + By + C = 0 Или с угловым коэффициентом y = x(-A/B) - (C/B) Параллельные прямые отличаются значением C.
Расстояние между параллельными прямыми = |C₁ - C₂| / sqrt( A² + B²)
Расстояние от точки (X,Y) до прямой |AX + BY + C| / sqrt(A² + B²)