Wasserman's neurocomputer technique: why does a three-layer network with three inputs form a non-convex area on a plane?

Question

Books

I started reading Wasserman's Neurocomputer Technique, got to three-layer networks and an example that shows how you can get a non-convex area. The book shows the following figure (Fig. 2.9):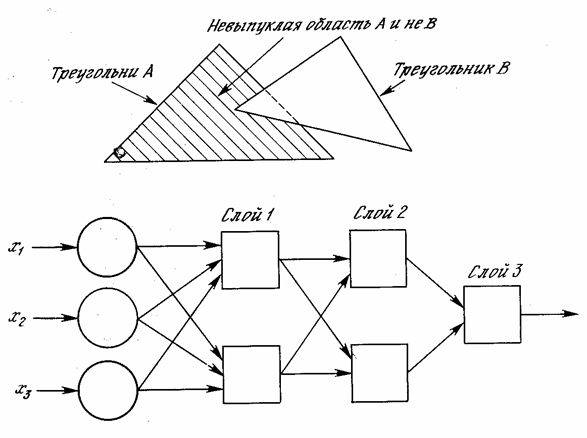

I do not understand how such a network configuration can form a non-convex area on the plane.
As I see the result of this network: 3 inputs - this is already a three-dimensional space. Each of the two neurons of the first layer divides the entire space into 2 half-spaces with planes. At the output of the neurons of the second layer, each of them allocates a convex non-closed region of space, bounded by two planes. Well, after the third layer it is possible to get a non-convex region of three-dimensional space.
And to illustrate an example from a book, there should probably be such a network: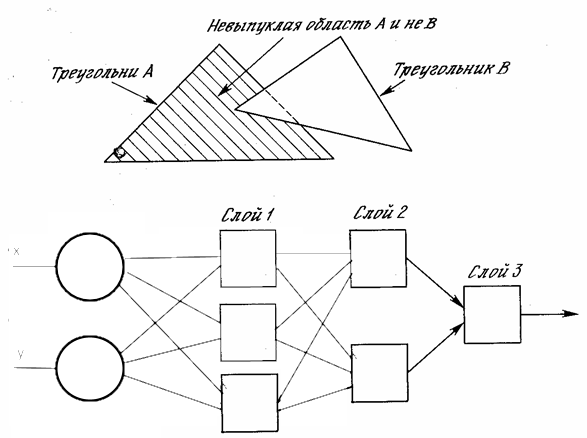

Where is the error in my reasoning?

Answer 1

stop smoking those mushrooms. but it won't let go)

Answer 2

here experts ask practical questions about how to upgrade to windows 10, and here you spam with your squares :)