Answer the question
In order to leave comments, you need to log in
Representing categorical and ordinal linear regression data (machine learning)?
I'm trying to fully understand the difference between representing categorical and ordinal data types when doing a regression. At the moment there are the following rules:
Categorical variable and example:
Color: red, white, black
Why categorical: red < white < black is logically wrong
Ordinal variable and example:
State: old, restored, new
Why ordinal: old < restored < new logically correct
Methods for converting categorical and ordinal data to numerical format:
Direct coding (display) for categorical data
Ordinal representation for ordinal data.
An example of converting categorical data into numbers:
data = {'color': ['blue', 'green', 'green', 'red']}
Number format:
id Blue Green Red
0 1 0 0
1 0 1 0
2 0 1 0
3 0 0 1id Data
0 0
1 2
2 2
3 1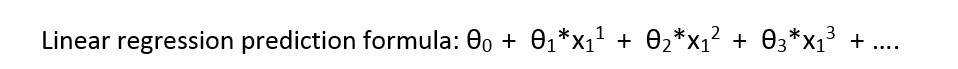
Answer the question
In order to leave comments, you need to log in
1. In fact, the whole machine comes down to solving optimization problems. There is a set of restrictions and there is a function that needs to be optimized (min, max). In your case, you are most likely minimizing the standard deviation. Divide the sample into two parts, study on the training, count the value on the control. This value is the quality criterion of your model.
2. If there are several models and it is not clear which one to choose. We need to divide the sample into three parts. In the first part, we train the models, in the second, we select the model with the best performance, in the third, we get the value of the optimized function on the winner of the previous part, the same quality criterion.
3. Conclusion: theory is good, but it's better to honestly compare models against data.
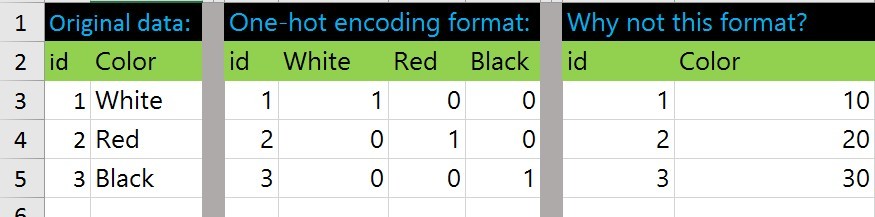
4. Theory. If you represent one category with several variables, then you get a large dimension. For example, if the color contributes according to the principle white - 0, red - 10, black - 20, then in one model it will be 10 * x_color, and in the other 0 * x_white + 10 * x_red + 20 * x_black. At the same time, the situation looks like white - 0, red - 10, black - 100, then in the first model the exact representation will no longer work, and in the second one you can still place the appropriate weights.
In essence, a model with many variables is a generalization of a model with one. The only problem is that the number of variables is growing...
Didn't find what you were looking for?
Ask your questionAsk a Question
731 491 924 answers to any question