Reed-Solomon code, why doesn't matlab want to output the correct generator polynomial?

Question

MATLAB

Hello, I'm trying to implement message transmission as in real radio navigation systems. There is a wonderful book "Aeronautical Telecommunications", which lists all the standards and message formats. From it I received information on how to supplement the message with a code that could later be used to recover the lost data, in fact, the Reed-Solomon code.
This is where the difficulties begin for me, I try to implement using Matlab.
Here is an excerpt from the book:

3.6.3.3.5 Application FEC. The application FEC is calculated using the application data using a
fixed length systematic (255, 249) Reed-Solomon (RS) code.
3.6.3.3.5.1 The field-defining primitive RS code polynomial, p(x), has the following form: 3.6.3.3.5.2 The

RS code generating polynomial, g(x), is described by: used to construct a Galois field of size 28, GF(256), and is the i-th primitive element in GF(256).

Here I immediately have a few questions:
1) Why i=120? Is there a reason for this?
2) How to open it so the brackets can be? I do not get you. I understood only about the free member - everything works out there and everything is fine, but how to count intermediate degrees? There negative $\alpha$ are obtained and I'm not very familiar with arithmetic in Galois fields to do anything about it.
Moreover, the book contains a gross translation error:

where is the square root of p(x)

But that's not the point, in Mathlab there is a very useful thing - Communications Toolbox to automate the process of generating Reed-Solomon code. And simply obtaining the degrees of a primitive element allows us to achieve the function

Код:
rsgenpoly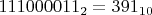

, where the actual parameters are the length of the entire message, the length of the useful message (i.e. minus the P-C code), the decimal notation of the primitive polynomial (In our case ) p(x), and the same i=120 whose origin and made me question.
In other words, I want to write:

Код:
rsgenpoly(255,249,391,120)

And get an answer

Код:
ans = GF(2^8) array. Primitive polynomial = D^8+D^7+D^2+D+1 (391 decimal)

Array elements = 

           1         176          186         244          176         156          225

But I get something completely different:
Code:

ans = GF(2^8) array. Primitive polynomial = D^8+D^7+D^2+D+1 (391 decimal)

Array elements = 

           1         217          99          62         217         130          23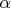

figured it out - this is a primitive element, matlab gives out the coefficients of the polynomial, and I want to get these coefficients, but expressed in terms of the degrees of the primitive element.
In order to make sure that the rsgenpoly function works correctly, I decided to take a look at the examples, took the book: "Simplification of the Reed-Solomon encoder using alternative simple polynomials that form extensions of Galois fields D.V. Kleiko, N.V. Lyamin". And drove some of the examples that are offered there. And the examples from the book work just fine.
now the question of choosing i=120 remains open. Everything else is already clear.

Answer 1

Try to read the materiel, and not guess on the coffee grounds, I especially liked what it is and why it is 120.