Answer the question
In order to leave comments, you need to log in
Physics of movement along a parabola. At what speed and at what angle should the body be thrown?
There are two tanks that shoot at each other. Between them there are obstacles and the highest obstacle is not always in the middle. It is necessary to make sure that the tank controlled by the computer hits the other tank as accurately as possible.
I tried to do it by eye and it turns out it is also very eye-catching. I set the angle so that the gun looks directly at the highest point and take a margin of 10 degrees.
Vector3 highestPoint;
Vector3 throwVector = highestPoint - gameObject.transform.position;
float anglef = Mathf.Atan2 (throwVector.y, throwVector.x) * Mathf.Rad2Deg - 10; // повернуть на 10 градусов выше
SetAngle (anglef);//время полета
// h - разница высоты между самой высокой точкой и текущим положением танка, т.е. расстояние, которое нужно преодолеть по высоте
float time = Mathf.Sqrt (2 * h / g);
// скорость, с которой нужно выпустить пулю
// S - расстояние, которое нужно преодолеть по координате X. Разница по х между текущим танком и танком игрока
float speed = S / time;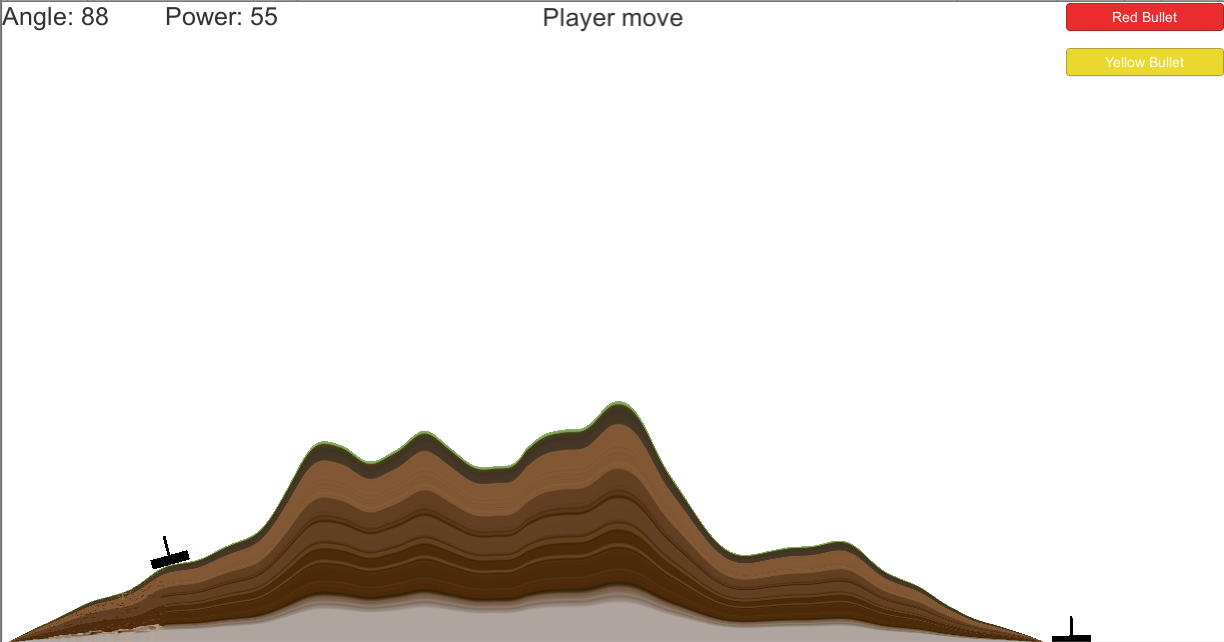
Answer the question
In order to leave comments, you need to log in
Let's solve the problem in two stages.
1. We will assume that we have only one peak of the mountain. The problem of constructing a parabola from three points. Two points - two tanks, the third point - the top of the mountain. Okay Google building a parabola using three points.
Decided.
2. Multiple peaks. Even from the available picture, it is difficult to determine by eye which of the two vertices is more important for our shot - the left one, or the one in the middle of the picture. So we need to define a list of vertices. There is scope for inventing an algorithm. For example, yes. We find the highest point, provided that it is higher than both tanks. Let's add it to the list. Next, a recursive traversal (here, we conditionally consider tanks to be vertices as well). Draw a straight line from the left (right) tank to the last vertex. We repeat the search for the maximum height, but we consider the height above the drawn line. The condition for exiting the recursion is that there are no points above the line. Thus found a list of vertices. For each vertex from the list, we solve the problem of constructing a parabola. Of all the parabolas, we choose the highest one.
Decided.
3... so, we wanted to solve it in two stages? But it was bare mathematics, and for the physical problem we got not quite what we needed. Suddenly. The decision would be correct if the tank could control the speed of the projectile. Then we could shoot at any parabola calculated above. But the tank has a fixed projectile speed (or am I behind the times?), and we only control the angle. Therefore, we must first solve the problem from a school physics textbook, about a shot from a cannon. The angle is determined without taking into account the mountains. In the general case, there will be two solutions, two possible angles - along a flat trajectory, and along a hinged one. We have a mountainous area, so the flat trajectory (angle from 0 to 45 degrees) does not suit us, there is one solution left. Those. the only chance to hit the target is to shoot with the angle found now, regardless of the location of the vertices. If there is a mountain in the way of the projectile, then the chances of hitting the target were exactly zero, at any other angle there will be a miss, even if we do not stumble upon a mountain. It turns out that all the reasoning at stages 1 and 2 was in vain? Not really. We can use them to determine whether the projectile will hit the mountain or not (with accurate aiming). If we find out what will hit the mountain, then we can not shoot, save the projectile, but this is already slightly beyond the abstract conditions of the problem.
It seems to be 10th grade, "body movement at an angle to the horizon"
Didn't find what you were looking for?
Ask your questionAsk a Question
731 491 924 answers to any question