Answer the question
In order to leave comments, you need to log in
Method of mathematical induction?
Help please, for the second day I have been suffering with these inequalities, if you wish, n still cannot be equalized to one
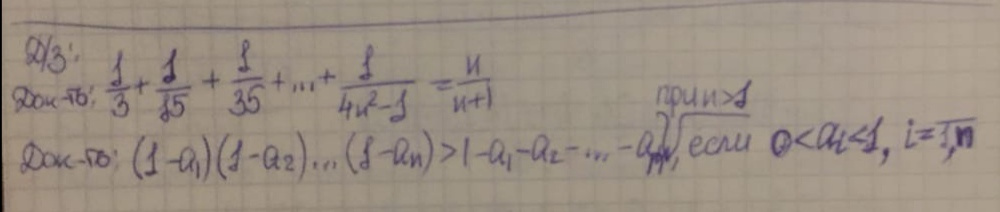
Answer the question
In order to leave comments, you need to log in
Perhaps the condition was rewritten incorrectly, or an error in the textbook. The first formula is wrong.
1/3 != 1/2
1/3+1/15 = 2/5 != 2/3
1/3+1/15 + 1/35 = 3/7 != 3/41/3+...1/(4n^2-1) = n/(2n+1)n/(2n+1) + 1/(4(n+1)^2 - 1) =carefully decompose the second denominator according to the difference of squares formula, reduce to a common denominator and factorize the numerator of the = (n+1)/(2n+3)FTD. (1-a1)(1-a2) = 1-a1-a2-a1*a2 > 1-a1-a2because a1*a2- is positive. Next, take the product for n, replace the first n-1 parentheses by the induction hypothesis, open the parentheses, and then you can omit all terms like ai*aj, they are all positive.
Didn't find what you were looking for?
Ask your questionAsk a Question
731 491 924 answers to any question