Learning math through programming, stupid decision?

Question

Programming

Hello. Well, without tedious ones, I studied poorly at school, right now I decided to take up my head.
Actually a subject, whether there is such variant?
I just decided to go hardcore right away deciding Scanavi for university applicants.
When solving on paper, I can't even solve a simple class 9 equation sometimes (rarely, of course, but this has happened).
And then the thought came to my mind, because each task is a clear algorithm, so you can try to solve it as all current programmers solve it after passing the university. On the computer. I took a python interpreter and found out that it is much easier for me to follow the sequence of actions of the author when solving an indicative example. Immediately everything more or less went smoothly, but on paper I lose my train of thought, I don’t know what the reason is. At what on a computer it is necessary to do even much more simplifications than on paper. That is, the algorithm grows into smaller pieces. Again, if it’s more convenient and understandable for me, is it possible to learn this way? Or will one day I just hit the ceiling and realize that it was all in vain? Am I in for such a surprise? You are smart people here, you know math. Applying it in your work, you first solve some complex equation on a piece of paper,

Answer 1

Until the problem is solved, it does not have a solution algorithm.
It happens that the problem is not solved. In this case, we must prove that there is no solution.
You can be smart without knowing math.
In the film "The Trap" the main character said: "There are always surprises."
Paper sometimes helps.

Answer 2

First, an analytical solution, then writing a program, moreover, taking into account the accuracy of calculations on a computer. Try to program in the forehead, for example, the following formula: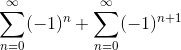

Answer 3

I am sure that the future lies with such an approach (for example, studying mathematics and physics through programming). The description of processes is well transferred to the programming language. The "programming" language itself, unlike the classical "algebra" language, for example, has a more applied and practical application, although in fact both languages ​​do the same -> that is, they describe the process / model / relationships.
for example, I also noticed behind myself that for me the description in the programming language is much clearer and clearer than the language of mathematics (simply due to the fact that I use it less often and understand it worse
) I see much more clearly what is happening and how, I can trace on my own where I have an error, and so on.
I'm not talking about modeling physical processes.
A sane understanding of physics came to me only through the programming of various game bots and processes.
======
About the process of writing code.
If the task is simple, then I usually immediately have a plan in my head, well, or after about ten minutes, for example.
In the form of an approximate solution scheme. I immediately sketch this scheme in the code, in the form of abstractions, without a clear implementation, then I start working on the implementations.
I try to visualize all the interconnection schemes (lower formulas) in my head without papers (it's faster and more convenient). But sometimes I sketch something on a piece of paper if I can’t imagine everything in my head.
I don’t use the language of mathematics much (only to describe simple relationships, such as a = 2b, etc.), but advanced research has to be read in mathematical language, which I admit is difficult for me. But it doesn’t bother me, because even so I’m a programmer and not a mathematician - my primary programming and development of software solutions, and not writing articles in scientific journals.

Answer 4

I would suggest teaching matesh the old fashioned way. According to the textbook and solving examples

Answer 5

In general, this is a normal situation.)))
I did not understand the proofs of theorems from geometry, did not memorize them until I began to break them into parts. we prove 1, we prove the second, and so on. Those. In order to understand a certain system, a person needs to break the system into parts. Understand how these parts interact. Then break the parts into sub-parts. and understand their interaction.
The same thing happens in programming. a function must contain parts one rung lower than itself. A person perceives this well and keeps it in working memory. If the parts are several steps lower, then confusion arises. And complexity.
For example, mathematical induction:
1 + 2 + 3 + 4 ... + n = n * (n + 1) / 2
the general algorithm consists of two parts
, there are some particular similar cases P.
1. we prove that if P(for the number m) is true, then it follows from it P(for the number m+1)
===n(n+1)/2+(n+1) = (n(n+1) +2(n+1))/2 = (n*n+3n+2)/2=(n+1)(n+2)/2
2. prove that the initial case P(1)
===1 (1+1)/2=1
The example has a general methodology in two parts. And there is one level below - proofs of particular formulas ===.
So it is in almost everything. That's how decisions should be remembered. Parts and interactions. + subparts and interactions. +...
For non-trivial tasks, the brain works a little differently. Little.
For further understanding of how to memorize and solve, I recommend the course
https://www.coursera.org/learn/learning-how-to-learn
it is free, in English, but with Russian subtitles.
It is led by a female mathematician who admits that at school she had no aptitude for mathematics. (so she thought)
she also has a book translated into Russian. There is a link in the course.
good luck.

Answer 6

I think it's a great idea. True, this may not be as easy as it seems.
It is quite possible to program the solution of equations of the square type, operations on matrices.

Answer 7

What do you consider to be the study of mathematics? Are you interested in any sections?
Mathematics consists of many sections. Some sections are closer to programming, others do not overlap at all.
For example, it will be convenient to learn linear algebra through programming. These are computer graphics, games and other fun things. I recommend "Coding the Matrix: Linear Algebra through Applications to Computer Science".
With mathematical analysis it is more difficult. Decide on a goal. To understand, you need to analyze the proofs of theorems, learn to reason. In programming, you can implement numerical algorithms for differentiation and integration, but this will not help in understanding the subject.
Try to start with linear algebra and classical mechanics in game development.