Answer the question
In order to leave comments, you need to log in
Is it possible to find the growth rate of a graph from a graph?
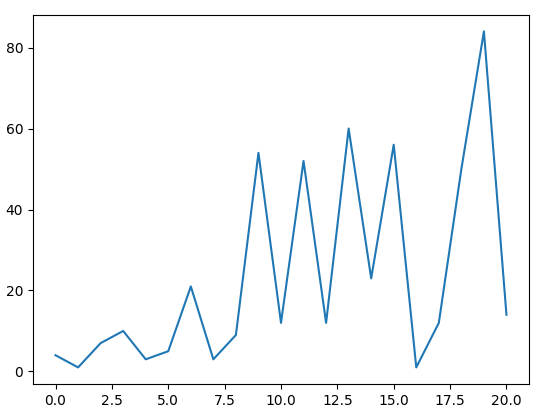
It is required to find the growth rate of the graph. How to do it? The graph consists of straight lines.
The output should also be a graph.
Is it possible to divide (y+10**-9)/(x+10**-9) ? 10**-9 - increment
Here is the result of these divisions (when x = 0, y turned out to be a very large number, so I replaced it with 0):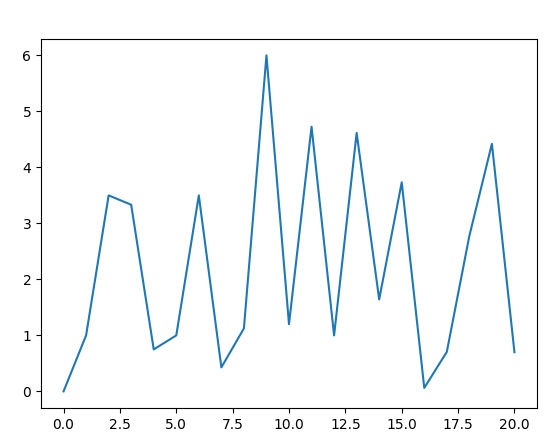
Answer the question
In order to leave comments, you need to log in
It seems to be quite simple. Draw vertical lines on top of the graph at breakpoints. You will see that the graph step is exactly equal to 1.
On each segment, the graph is straight, which means that its growth rate dx / dyin the segment is constant. Its value is simply the difference between Ythe start and end of the segment (because the width is 1).
Therefore, the steps can be drawn directly on top of the segments - so that they are the diagonals of the steps.
And then move these steps to the axis OX, above or below it, depending on the sign. Something like this:
If there is data on which the first graph is built, it’s generally wonderful. The Xstep is equal to 1. Hence, the growth rate is equal to the difference Yat the ends of the segment.
For example, giveny = [1,3,9,2]
Didn't find what you were looking for?
Ask your questionAsk a Question
731 491 924 answers to any question