How to get circle coordinates?

Question

Mathematics

How to get N coordinates around a circle within a radius of 1km?

For example:
There is a point with coordinates: 55.754755, 37.620584
And I need to get the N-th number of points along a radius of 1 km.

In my case, these are the coordinates of the earth's surface:


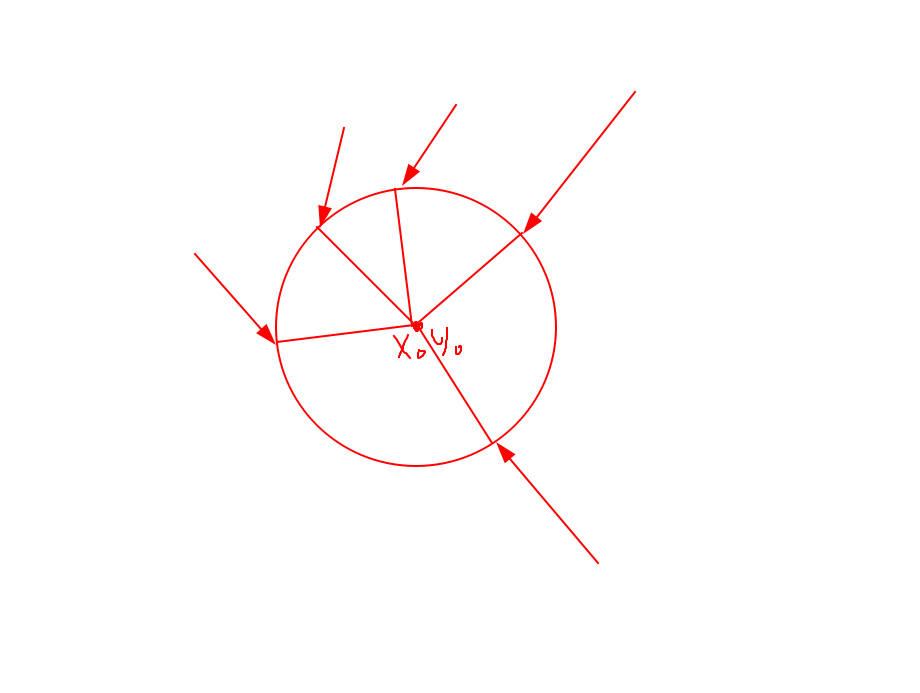
I need to get several points on the circle (marked with lines).

Answer 1

It is necessary to use the Vincenty formulas for solving direct and inverse problems.
Straight: Based on the current latitude, longitude, bearing and distance, calculate the coordinates of another point.
Inverse: given the coordinates of two points. It is necessary to calculate the distance between them and the azimuths.
You need to solve a direct problem.
https://en.wikipedia.org/wiki/Vincenty%27s_formulae
https://movable-type.co.uk/scripts/latlong-vincent...

Answer 2

You need polar coordinates
Formulas to translate:

x = x0 + R*cos(phi)
y = y0 + R*cos(pi/2 - phi) = y0 + R*sin(phi)

They are based on the fact that the projection of a vector onto an axis (or, in general, a direction) is the length of the vector multiplied by the angle between the axis (or direction) and the vector. The angle is counted counterclockwise from the direction to the vector. If the angle is "uncomfortable" (more than 180 degrees, for example), then it still needs to be taken. Well, or take a smaller "convenient" angle and take into account the projection direction in the formula - if the projection direction coincides with the positive direction of the axis, then put "+", if in the opposite direction - then "-".
And so - set any angle and get any number of points
. For the Earth's surface, in general, spherical coordinates are needed, and more precisely, the intersection with a paraboloid. But for 1km it is quite possible to try to limit yourself to this