How to uniformly render tree nodes?

Question

infographics

There is an arbitrary tree, sibling nodes are separated from each other by a dynamically set value (in this case 20), as well as neighboring nodes (in this case 40). At the moment when the leftmost branch is formed, the node arrangement method is called to which the top-left and top-right are passed and the difference by which the gap between them has increased (in this case 20).
Here's what happens in the node arrangement method -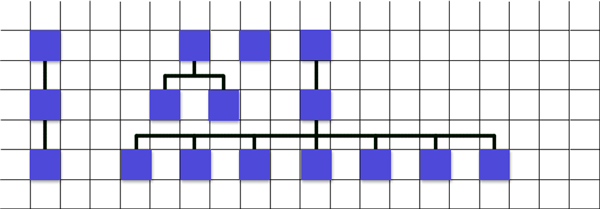

1. in the cycle we go from top-left to top-right and count the gaps (in this case, these are six empty cells, which, as I said earlier, are 20 each, that is, the sum is 120);
2. divide the amount obtained in the previous step by the number of nodes plus one (120 / 3 = 40);
3. I check how far the current node (I start from left to right and therefore the current node is the one with two children) is removed from the left sibling node (in this case it is 80).
4. now I subtract from 80 - 40 = 40, this is the distance by which I will move the current node to be in the right place.
5. if this value (40) is greater than the one by which the distance between the two extreme nodes has increased, then this value becomes smaller. That is, I calculated that 40, but it is more than allowed, and therefore the value changes to 20.
6. I move the node.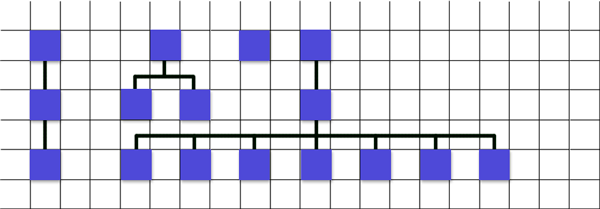

Repeat the previous six steps for the next node -
1. get 60
2. 60 / 2 = 30
3. 40
4. 30
5. 10
6. ...

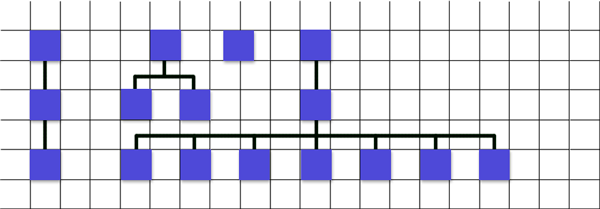
See how I averaged? First I figured out that I need to shift by forty, but since I can’t shift by forty (the rule for the lower children will be violated, they will be closer than forty), I shift to the maximum possible, this is twenty. And then I shift by ten.
For example, if the first processed node had no children, then the picture would be as follows -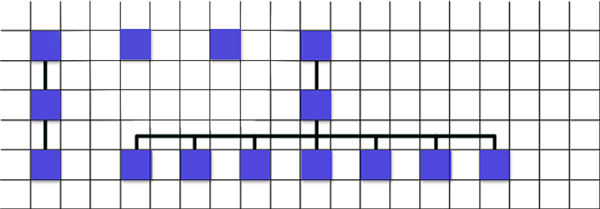

In case I first have a node that can be moved by "some" (without children), and then one that can no longer be moved by "something", then I again shift the second to the maximum, but at the same time I execute the algorithm from the very beginning (more precisely, from the very last successful point), but for a while I replace the top-right one with the current one.
I would show the code, but I do not want you to look at its shortcomings, but I just want you to understand the meaning.
Here. But then I ran into the following problem, and perhaps this is only one of them ...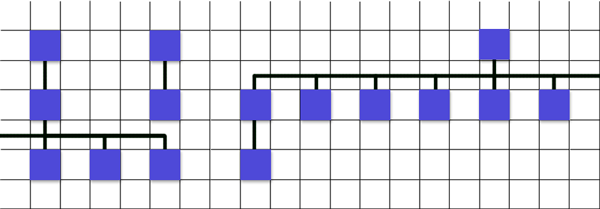

The input data is the same, but everything breaks. The algorithm, as I wanted, did not work out, and I cannot think of it.
What do
indent nodes have - the value by which the current node is removed from the previous one |_|->|_|
leftOffset is the value I'm shifting to the left. At the very beginning it is zero
rightOffset = this is the value by which I shift to the right. And also zero by default.
Here. The nodes themselves, like ordinary nodes, are a reference to the parent in which they are stored in an indexed array. There are methods for getting a node by index and getting the index itself.
If there are any ideas, I will be glad to listen, I myself just have a universal emptiness in my head.

Answer 1

Thank you for inviting me, I'll help in any way I can.

sibling nodes are separated from each other by a dynamically set value (in this case 20), as well as neighboring nodes (in this case 40)

Let's define the terminology, do we mean by neighbors nodes at the same level of the tree that do not have a common immediate parent (not brothers)?
Unfortunately, I did not fully understand your algorithm, if I have time, I will try to repeat it later. But the idea of ​​moving individual nodes "manually" does not appeal to me.

If you have any ideas I'll be glad to hear

The idea is this. A tree typically has more nodes at lower levels than at higher levels. More nodes - less freedom in terms of any uniform placement of them. So start at the bottom. Of the ready-made algorithms, I can only recall Tidier drawing of trees (by Reingold, Tilford), it is quite possible that it will be possible to adapt it to your requirements.