Answer the question
In order to leave comments, you need to log in
How to solve a problem using dynamic programming?
Hello.
There is such a problem and it is impossible to solve. There are similar ones on the Internet, but either the solution algorithm is not fully described there, or it’s not clear to me what and how. I tried to solve problems on paper, but nothing worked.
It is enough for me to simply explain in detail the solution algorithm or key points, the code is not needed
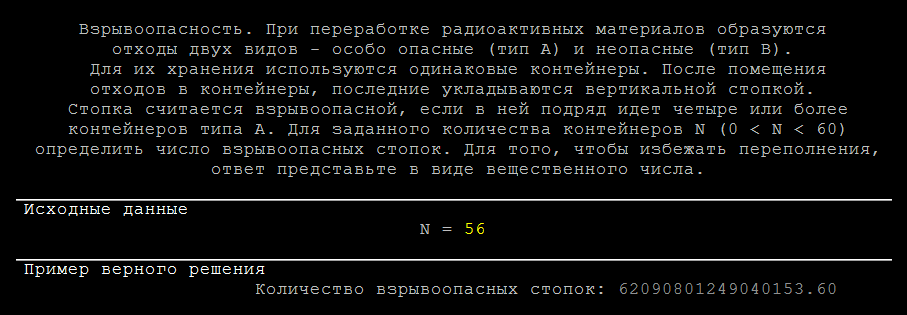
Answer the question
In order to leave comments, you need to log in
Some idiot made up the problem.
First, for N<60, the answer is placed in a 64-bit integer type, which is now available in almost all programming languages. There is no need to invent anything to avoid overflow.
Secondly, in order to avoid overflow, in such problems they are usually asked to give the answer modulo some large one. And finally, how the answer can turn out to be non-integral is just a mystery. The solution example is clearly wrong.
And so, dynamic programming is simple here: Let F(N,K) - how many non-explosivestacks of length N such that there are exactly K dangerous containers at the end (obviously 0 <= K < 4). This is not exactly what you need in the problem, but the number of dangerous stacks is the number of all stacks (2^N) minus the number of non-explosive ones, so this DP suits us.
The conversion is very simple:
F(N,K>0) = F(N-K,0)
F(N,0) = F(N-1,0)+F(N-1,1)+F(N-1,2)+F(N-1,3)F(0,0) = 1, F(0, K>0) = 02^N - F(N,0)-F(N,1)-F(N,2)-F(N,3)
Didn't find what you were looking for?
Ask your questionAsk a Question
731 491 924 answers to any question