Answer the question
In order to leave comments, you need to log in
How to search for a function by known values?
Suppose there is a set of known numbers:
a1, b1, с1, R1
a2, b2, c2, R2
...
an, bn, cn, Rn
Rn = F(an, bn, cn).
The task is to find the form F from the known sets {an, bn, cn, Rn}.
Tell me in which direction to dig, I forgot mathematics from the institute ...
Answer the question
In order to leave comments, you need to log in
You are interested in Feature Selection. en.wikipedia.org/wiki/Feature_selection . Where to dig further, now I can not tell. If you are just interested in dimensionality reduction, and not which feature is more important, then you can use PCA. The most popular algorithms are implemented in Machinle learning libraries like WEKA.
Google function approximation, function interpolation
en.wikibooks.org/wiki/%D0%98%D0%BD%D1%82%D0%B5%D1%...
Based on a known set of points, one can only assume the type of function, for example, the set (-1, 0), (0, 0), (1, 0) can belong to both the straight line y=0 and the sinusoid y=sin(πx) or the polynomial y =x 3 -x . Usually, the type of function is selected from the physical model of the process for which the data is obtained.
In fact, in the sets {a1, a2 ... an} there are not 3, but somewhere around 50 values, i.e. F is a function of a bunch of variables. Sets (a1, a2 .. an, Rn) can be calculated any number of times (the program calculates using a formula unknown to me).
In fact, the task is rather the following. When some variables change, the value of F changes little or does not change at all (there are many such variables). It is necessary to find variables that do not affect / greatly affect the value of F. That is, there are 2 arrays:
{a1, a2 .. an, F()=R1}, {b1, b2 .. bn, F()=R2}
and you need find a correlation between them.
If at least the general form of the function is not known in advance, then, in my opinion, it is easier to disassemble the program and understand the calculations than to try to determine the interdependencies between 50 parameters. For example, for such a function of two variables, the
dependence on y is strongly manifested only in a small range of x values around x=b . But a function can also be piecewise continuous, for example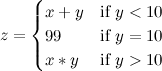
Didn't find what you were looking for?
Ask your questionAsk a Question
731 491 924 answers to any question