How to program the probability sum formula?

Question

Algorithms

Hello! Shame and disgrace, but what can you do :-)
Everyone knows the formula for the probability of the sum of joint independent events:
P(A+B) = P(A)+P(B)-P(A)*P(B)
is the formula for the sum of n events, which is built by analogy

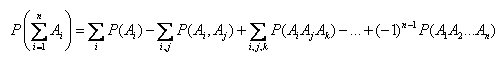
: events are independent, then all the probabilities of the products are equal to the products of the probabilities.
I don't understand how to program it. Those. the task is to write a function that takes as an argument an array of probabilities A1...An, the actual number n, and which returns the probability of the sum.
I understand C++, Delphi :-)

The title is obviously this:

float getChanceSumm(float * arr, int n){
    //OMG
}

The task can be reduced to writing another function - getting the sum of all combinations of k elements without repetitions, but this does not make it any easier.

People, help! :-) Thanks in advance. On Friday, the brains are not the same. I hope only I have

UPD: the amounts that in the general formula do not go for all indices, but only for non-repeating ones.

UDP2:

Thanks to the hint of the respected Ents , this simple function turned out:

float getSummChance(float * arr, int num){
  float res,temp;

  if (num==1){
    res = arr[0];
  }else
    if (num==2) {
      res = arr[0]+arr[1] - arr[0]*arr[1];
    }else{
      temp = getSummChance(arr,num-1);
      res = arr[num-1]+temp - arr[num-1]*temp;
    }

  return res;
}

Maybe it will be useful for someone else to calculate the probability of the sum of joint independent events, so despite the fact that this question is a shame to my bald head, I still will not delete it :-)

Answer 1

In such a formulation of the problem (the sum of joint and independent events), it is much easier to switch to opposite events and use the formula

Use it to your health :)

Answer 2

write a recursive function
P(A1, A2, A3, A4, ..., An) = P(A1) + P(A2, A3, A4, ..., An) - P(A1) * P(A2, A3 , A4, ..., An)

Answer 3

P(A+B) = P(A)+P(B)-P(A)*P(B)
This is a formula for independent events only.
For dependent events, your second formula is correct (for n events), which for two will be:
P(A+B) = P(A)+P(B)-P(A*B)
or
P(A+B) )=P(A)+P(B)−P(A)*P(B∖A)