How to minimize a logical equation?

Question

Mathematics

There is such an equation:


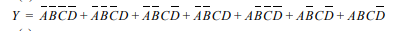
Here is the final minimization:


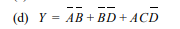
Tell me how to step by step from the first to come to the second type of equation.

In the course of solving, I reach the moment when the left and right parts of the minimized equation can be obtained, but it is not clear where the middle part comes from.


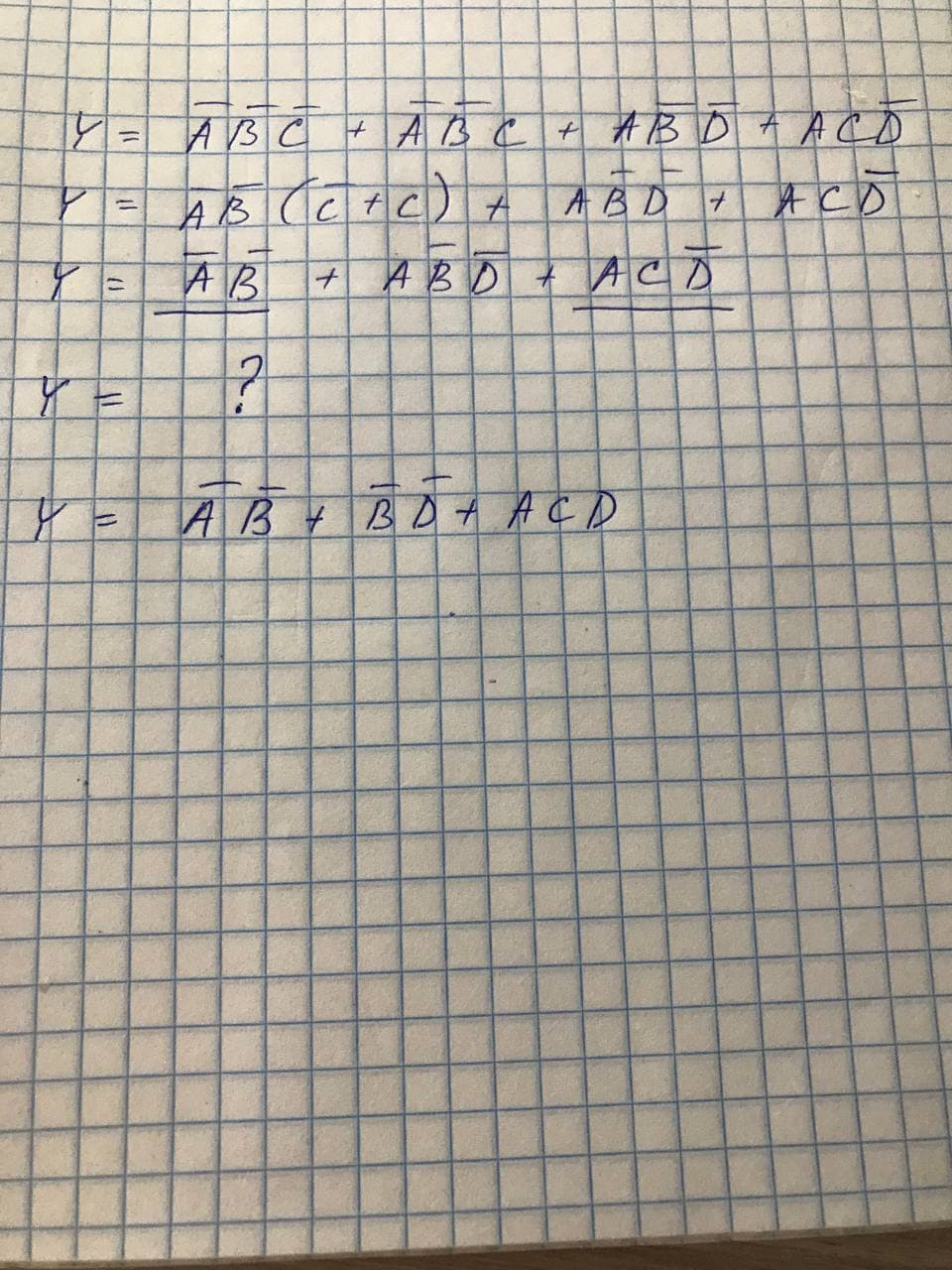
UPD: in the last line D with dash

Answer 1

You didn't lose C in the third term in the first line.
And then there will be 2 adjacent terms A !B !C !D+AC !D. Here you can take A !D out of brackets and it will remain (!B !C+C). This can be shortened simply to !B + C. There was such a rule, it seems, but it can be proven. If C is true, then the original is already true. If !B is true, then either !C is true and the first term is true, or C is true and the second term is true.
Now the third term has abbreviated then A !B !D
Then repeat the trick, taking out the brackets from the first and second terms !B. There will remain !A+A !D = !A + !D