How to inscribe a circle between two sides of a triangle and an arc?

Question

Mathematics

It was required to fit a circle into a non-standard figure.
My construction was as follows:
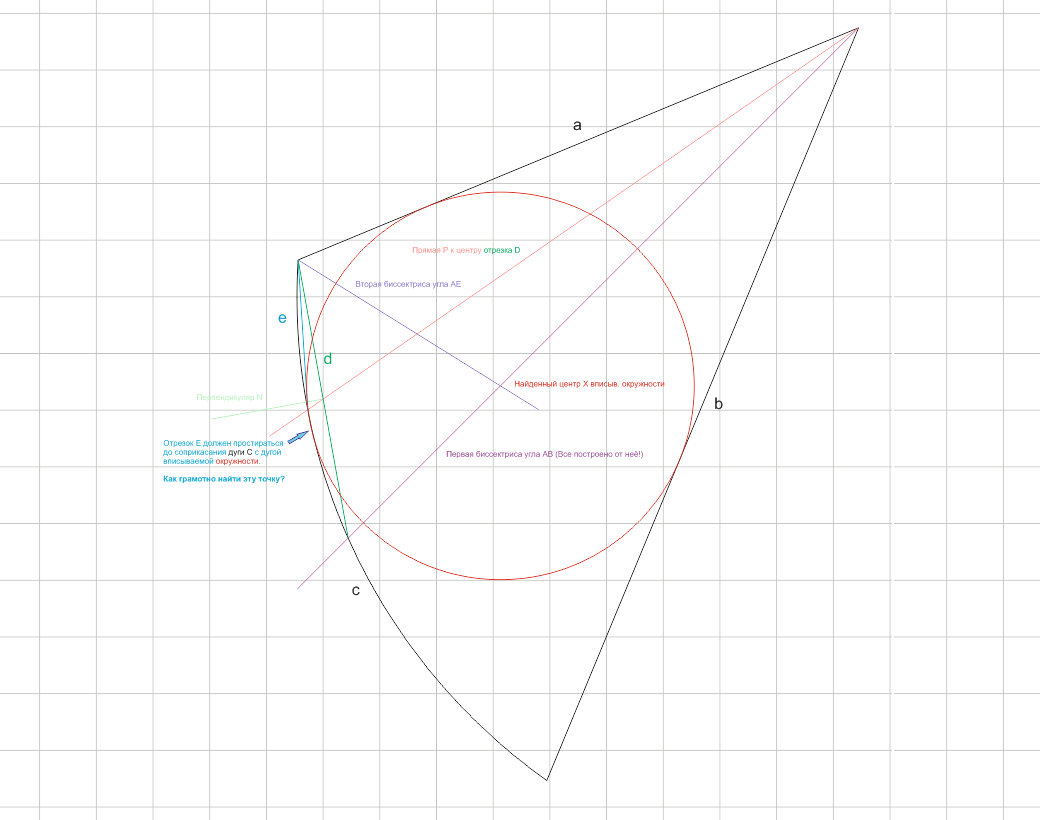
1. Draw the first bisector from angle AB;
2. Draw segment D from angle AC to the intersection of arc C by bisector AB;
3. Draw a line P from angle AB to the center of segment D;
4. Draw segment E from angle AC to the intersection of line P of arc C;
5. Draw a second bisector from angle AE;
6. At the intersection of two bisectors, the approximate center of the inscribed circle is found.
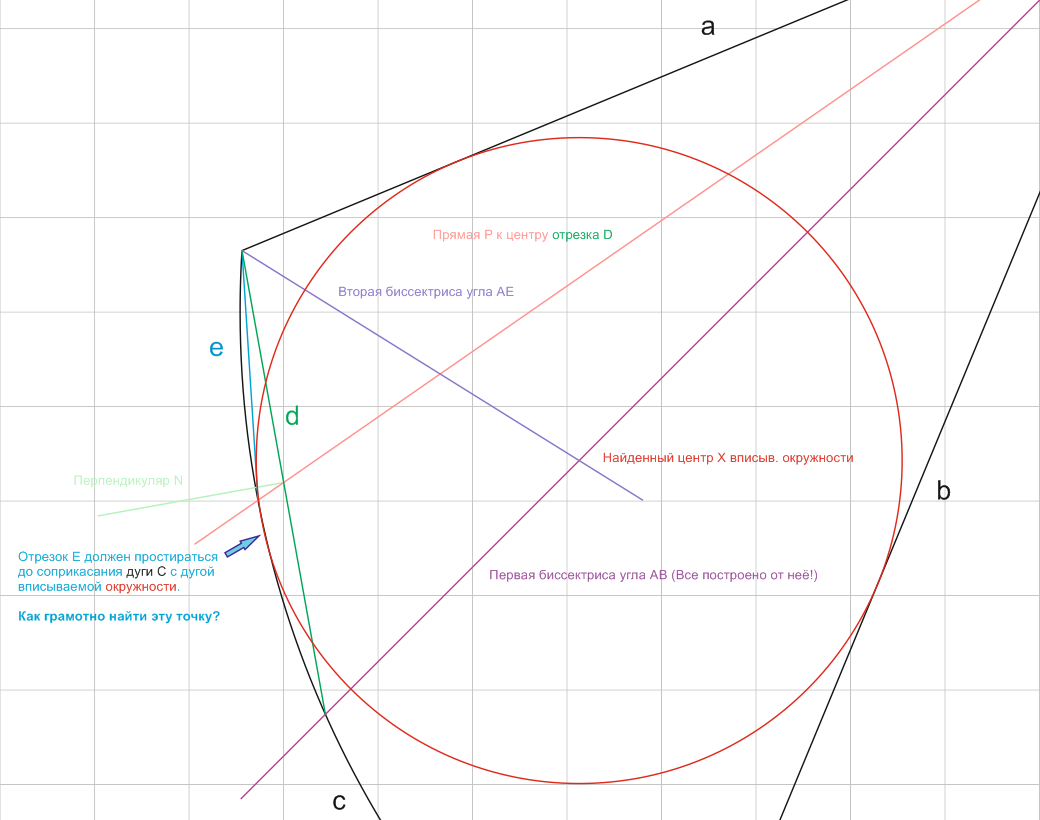
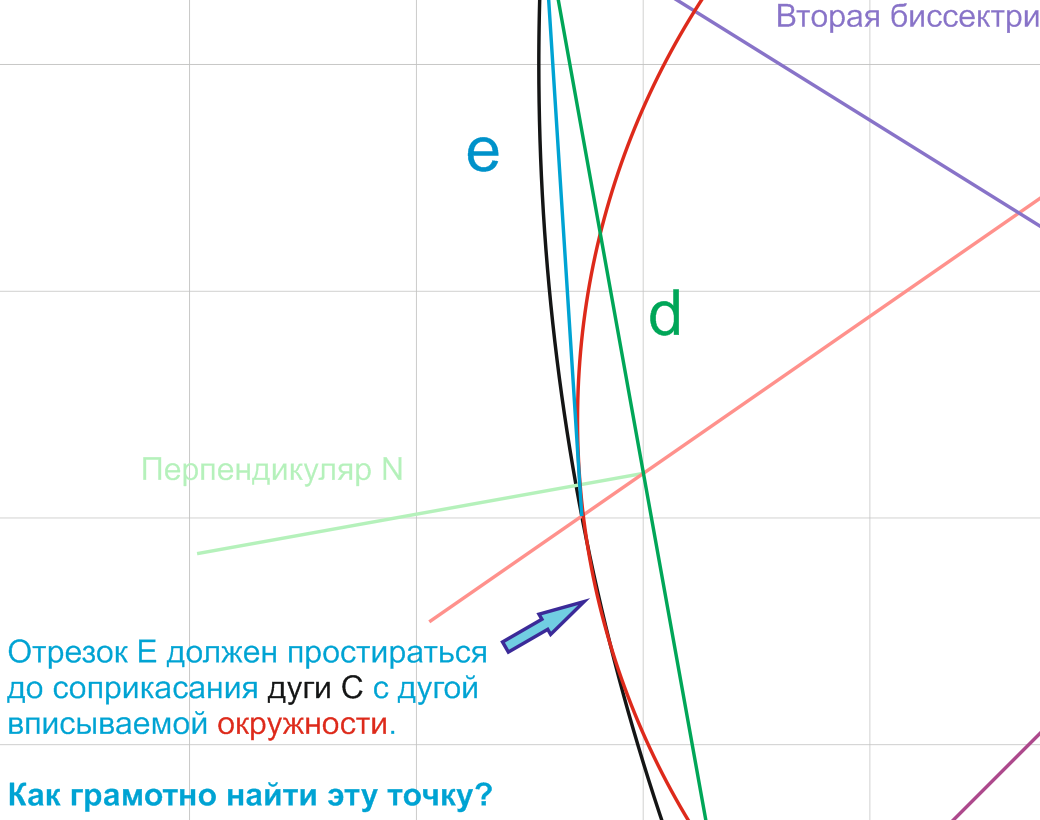
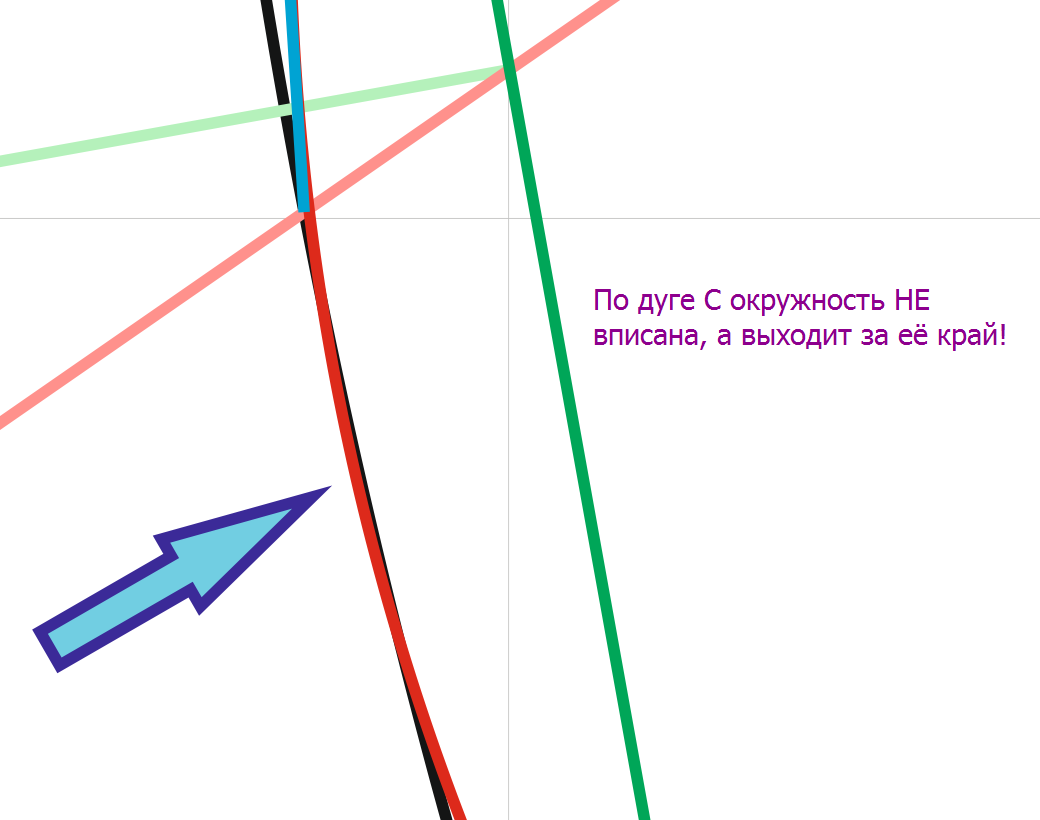
But it's not accurate... It's not accurate in terms of inscribing the circle into the arc C. The arc of the circle hangs over the edge of the arc C.
This construction can be seen in the attached screenshots.
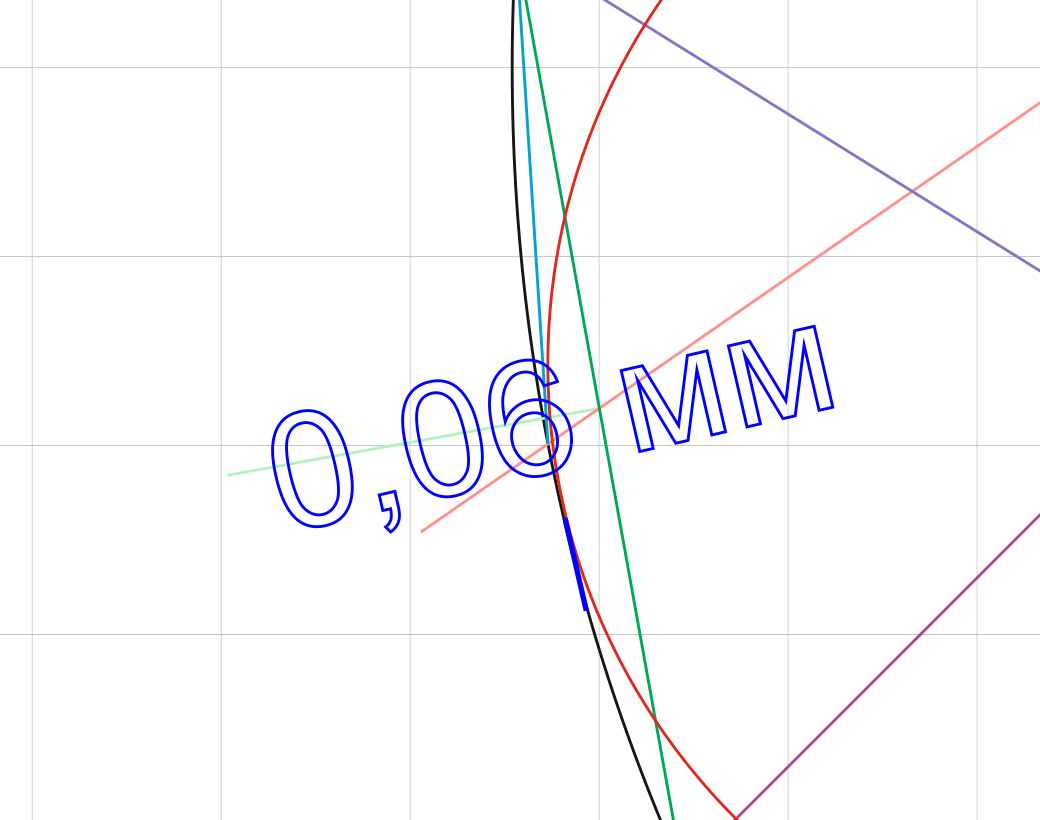
How can one understand that on sides A, B the circle is inscribed, but on arc C, the circle hangs over the edge of arc C. And the discrepancy is 0.06 mm (with a diameter of the inscribed circle of 34.18 mm). This is also demonstrated.
That is, what I did is only an approximate, erroneous solution. Close to correct, but definitely not 100%.
Hence the question: how to geometrically correctly inscribe a circle in a given figure? More precisely, how to find this point on the arc C, to which we can draw the segment E?
My thoughts:
In fact, the blue segment E should extend to the center of the area where the arc C and the circle overlap each other. Then the bisector from the segment E, more precisely, from the new angle EA, will find the exact center relative to the arc C.
That is, if the segment E is extended further, to the center of the region of overlapping overlapping of the arc C and the circle on each other, then the angle between the segment E and side A will be smaller, therefore, the intersection point (the center of the future inscribed circle) of the two bisectors will be mathematically and physically further from the arc C. And then the circle will be inscribed in the arc C. I
also thought that finding this point is something from the area of ​​​​the graph of the decreasing function f (x) ...
***

***

***

***

***

***

***

Answer 1

Finding the center of a circle along an arc is not difficult. So it will start from there. Triangle DCE is given, where CE is an arc of a circle with center A. Moreover, point D lies on the left side of the vector EC.
Constructions in geogebra
Restored the construction in algebra, so it is very likely that there is a simpler solution.