Answer the question
In order to leave comments, you need to log in
How to increase the height of a rotated rectangle mathematically (quick algorithm)?
In the 2D coordinate system, there are 4 points that define the coordinates of a rectangle rotated by an unknown angle. It is necessary to increase the height of this rectangle by a certain scale factor and get new coordinates of the vertices. Please advise how to do it and do it, preferably quickly (with a minimum of trigonometric functions).
A,B,C,D are given - you need to find A1, B1, C1, D1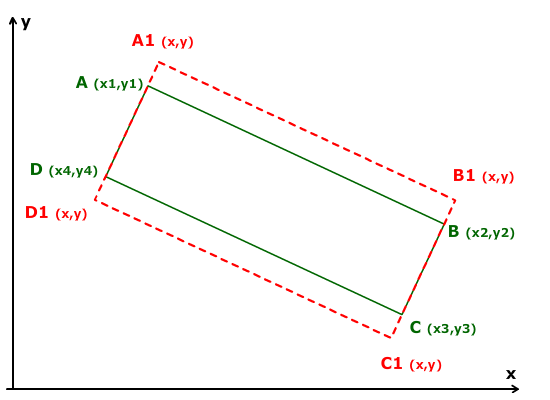
Answer the question
In order to leave comments, you need to log in
M AD = ((x 1 + x 4 )/2, (y 1 + y 4 )/2)
A' = M AD + (A - M AD ) * scale
B' = M AD + (B - M AD ) *scale
When drawing rotated shapes, you can apply affine transformations. The computer can do it quickly.
For example, when drawing a rectangle, we draw it non-rotated (sides are parallel to the edges of the screen), set the transformation matrix (which determines the offset, rotation, scaling in X and Y), and now we already have the rectangle we need in the right place at the right angle.
If you need to compress/stretch, you can trivially compress/stretch the original rectangle (not rotated). Its transformation matrix will remain the same and will shift/flip it to where it was originally, but already squashed/stretched.
Or you can modify the transformation matrix accordingly. The transformation matrix determines, among other things, the expansion / compression along the axes.
In .NET, GDI+ has ready-made features for working with affine transformations:
Matrix representation of transformations
Using transformations in managed GDI+
PS:
If your task is a laboratory from the cycle: done and forgot, then all this fuss does not make sense.
But in large projects, where there are many graphical elements rotated relative to each other and hierarchically connected, it is better to master the mathematics of affine transformations and rebuild the architecture in accordance with them. It will be easier to live.
1) find the midpoint of the segment AD - the arithmetic mean of x and y
2) for simplicity, we will consider the midpoint of the segment as the origin of coordinates
3) find k, which from the equation of the line y = kx: k = y1/x1
4) solve the system:
- y = kx
- sqrt(x^2 + y^2) / sqrt(x_1^2 + y_1^2) = scale
You can use the formula for dividing the segment in this regard (the first link that came across ). As suggested by Stanislav Makarov , first we find the seridine AD, denote it by M. Next, we consider the segments MA and MD (the order of the points is important), and apply the formula for dividing the segment with respect to lambda < 0 (some negative number, an analogue of your scale). We do a similar procedure with BC.
UPD. Point M, by the way, is also obtained by the formula for dividing segment AD in this respect with lambda=1.
Didn't find what you were looking for?
Ask your questionAsk a Question
731 491 924 answers to any question