2D Discrete Fourier Transform for Image (very big question - lots of text)?

Question

Mathematics

Essence of the issue:
There is a binarized black and white image obtained after several stages of processing the original image using filtering methods in the spatial domain - a unified employee profile - black printed text on a white background and a black and white photograph in the corner of the document. Also, in some places, the background of the document has artifacts - "spots" of gray color - areas of pixels on some part of the image. Artifacts of gray color can be present both on a pure background and serve as a background-substrate in the text area - that is, in its main part - the text on a white background, but some of the letters, words can be on a gray "spot". It is required to filter the image in the frequency domain.
Background and some clarifications (please don't skip):
the first stage of frequency filtering will be the transition to the frequency domain using the DFT (I know that for adequate calculations you need to use the FFT, but I will figure it out step by step). I read about the DFT, in fact, as well as about image processing in the book "The World of Digital Image Processing" - S. Gonzalez, R. Woods. Let me just make two points:

1. Before that, I didn't deal with image processing.
   
2. Not familiar with DSP
   

- all the "knowledge" for solving the issue (including the mentioned spatial filtering methods that were applied to the original image), so far I'm reading from the above book.
It should also be noted that I know that there are ready-made libraries for FFT and DFT, just one of them, after many unsuccessful attempts to implement the DFT "by hand" - I used - the AForge.Imaging library ( www.aforgenet.com/aforge/ framework - the site of the framework.) The library copes with its tasks, but I only get an image of the Fourier spectrum, but I need the converted values ​​of the points (image pixels) for the frequency domain - for their subsequent use. In summary, why this library does not quite suit me:

1. The library outputs only the Fourier spectrum in the form of an image, without the ability to use the "raw data" of the transformation from the spatial to the frequency domain
   
2. The library is a "black" box, which makes it impossible to experiment in order to "twist and see what's going on" (I, as a beginner in all this, really need it - no one says to write bicycles all the time, but to understand a new area of ​​\u200b\u200bwork - necessary)
   

- regarding claim No. 2 - in the future, I will need to perform homomorphic filtering, where I need to transfer ln from the pixel value to the DFT, or to perform the DFT over the entire image after full brightness logarithmic filtering, but I would like to be able to write a DFT function that allows you to transfer not only the whole image, but also to transmit individual pixels.
The essence of the problem:
In order to deal with the two-dimensional case - I started with something simpler - with a one-dimensional DFT for a wave (sonic or something else), I found two such examples:

/////////ДПФ
double Re = 0, Im = 0, summaRe = 0, summaIm = 0, Ak[512] = {0}, Ak_1[512] = {0}, Arg = 0;
for (int i = 0; i < 512; i++){
summaRe = 0; summaIm = 0;
for (int j = 0; j < 512; j++){
Arg = 2.0*M_PI*j*i/512.0;
Re = cos(Arg)*(massiv[j]);
Im = sin(Arg)*(massiv[j]);
summaRe = summaRe + Re;
summaIm = summaIm + Im;}
Ak[i] = sqrt(summaRe*summaRe + summaIm*summaIm);}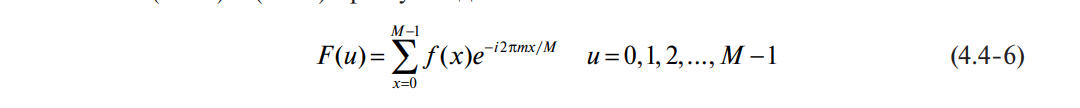

512 samples are set according to the condition of the original question - I'll replace it, let's say with the width of the image (if we imagine the image as a single strip (vector) of pixels). As I understand it, according to this formula from the book:

for the one-dimensional case of the DFT, there are two cycles - one for counting the points of the transformation itself and one for the sum of the values ​​for each point.
Also, in principle, I understand where the sines and cosines come from (yes, I know that the DFT is, in fact, the expansion of the signal into harmonics, but I’m more about mathematical notation):

Another found example, in C #:

public class FurieTrans { 
        public List<Complex> koeffs; 
        public double K; 
        public FurieTrans() { 
            koeffs = new List<Complex>(); } 
        public void dpf(List<Point> points, int count)  { 
            koeffs.Clear(); 
            K = points.Count; 
            //Цикл вычисления коэффициентов 
            for(int u=0; u<count; u++) 
            {  //цикл суммы 
                Complex summa = new Complex(); 
                for (int k = 0; k < K; k++)  { 
                    Complex S = new Complex(points[k].X, points[k].Y); 
                    double koeff = -2 * Math.PI * u * k / K; 
                    Complex e = new Complex(Math.Cos(koeff), Math.Sin(koeff)); 
                    summa += (S * e);   } 
                koeffs.Add(summa/K); }  } 
        public List<Complex> undpf()  { 
            List<Complex> res = new List<Complex>(); 
          for(int k=0; k<K-1; k++)   { 
                Complex summa = new Complex(); 
                for (int u = 0; u < koeffs.Count; u++ )  { 
                    double koeff = 2 * Math.PI * u * k / K; 
                    Complex e = new Complex(Math.Cos(koeff), Math.Sin(koeff)); 
                    summa+=(koeffs[u]*e);  } 
                res.Add(summa);   } 
            return res;  }  }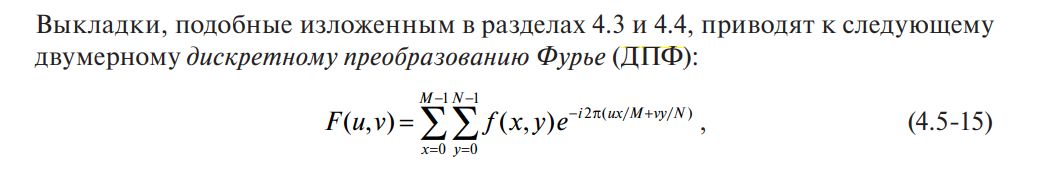

Now, based on all this and the formula from the book for the 2D DFT event:

- here's what I got:

static void MakeFurieTransform(FT_mode mode)  {
            Bitmap FFT_bitmap = new Bitmap(workBitmap.Width, workBitmap.Height);
            double realPart = 0, imagePart = 0, rotAngle = 0, amplitude = 0;
            double e = 0;
            double summ = 0;
            if (mode == FT_mode.direct)  {
                for (int u = 0; u < workBitmap.Width; u++) {
                    for (int v = 0; v < workBitmap.Height; v++) {
                        summ = 0;
                        //циклы суммы
                        for (int x = 0; x < workBitmap.Width; x++)  {
                            for (int y = 0; y < workBitmap.Height; y++) {
                                double Rot_coefficient = -2 * Math.PI * (u * x / workBitmap.Width + v * y / workBitmap.Height);
                                realPart = Math.Cos(Rot_coefficient);
                                imagePart = Math.Sin(Rot_coefficient);
                                e = realPart + imagePart;
                                summ += workBitmap.GetPixel(x, y).ToArgb() * e;  }  }
                        //формируем Фурье-спектр
                        amplitude = Math.Sqrt(realPart * realPart + imagePart * imagePart);
                        rotAngle = Math.Atan(imagePart/realPart);
                        int_R = (int)amplitude;
                        NormalizePixel(ref int_R);
                        FFT_bitmap.SetPixel(u, v, Color.FromArgb(int_R, int_R, int_R));   }  } }}

Actually, the question itself:

1. Where I get the value of e - e = realPart + imagePart;- what to do with the complex part of i near the sine? Those. e^iAngle=cos(Angle)+ i sin(Angle) - what to do with the imaginary part during implementation?
   
2. Here:

   amplitude = Math.Sqrt(realPart * realPart + imagePart * imagePart);
                           rotAngle = Math.Atan(imagePart/realPart);
                           int_R = (int)amplitude;
                           NormalizePixel(ref int_R);
                           FFT_bitmap.SetPixel(u, v, Color.FromArgb(int_R, int_R, int_R));

   - I don't quite understand what should serve as the new pixel color value. Am I doing the right thing?
   

PS
Used sources:
Code example #1 - https://www.cyberforum.ru/cpp-builder/thread860204.html
Code example #2 - https://www.cyberforum.ru/digital-signal-processin...
What read, in addition to the book:
https://habr.com/ru/company/otus/blog/449996/
psi-logic.narod.ru/fft/fft.htm (not all of the table of contents - only the first sections with theory)
Some questions that may arise:
1. Examples of source images/received spectrum? - no, unfortunately I can’t post it (I can’t post the spectrum - because it can be used to restore the original image)
2. Why "that's all"? - 1. I study like everyone else. Therefore, I run into a haystack with a rake. 2.Fmnalnaya goal "that's all" - the preparation of the original image (rather specific) for OCR.
3.Why c# and not, for example, C++? - I know a little C#, so I chose it; it's easier to read / write when learning in a new area , which allows you to concentrate on a theoretical problem, and not on memory tracking - like in C ++ (subjectively) (yes, for a bad programmer, distribution interferes with memory) + it is easier to cut the same Tesseract OCR (also subjective).
4. Why work with images, partly DSP, and stick to this OCR, and not, for example, neural networks or *substitute your own version*? I don't know, honestly, I don't know. I have not worked with images or neurons before, therefore, I decided to go somehow like this "classic" way of processing images using filters.
5. Maybe all this is not necessary and focus on different OCR libraries? - maybe, but I tried to feed the original image as input for both Tesseract OCR and IronOCR - the result, frankly, is sad.

Answer 1

Very interesting, nothing is clear.

Where I get the value of e - e = realPart + imagePart; - what to do with the complex part i near the sine? Those. e^iAngle=cos(Angle)+ i sin(Angle) - what to do with the imaginary part during implementation?

If you only want the frequency spectrum, you can just throw out the other part, but then the inverse conversion is not possible.

I don't quite understand what should serve as the new pixel color value. Am I doing the right thing?

You have to get the frequency-phase spectrum, cut out unwanted frequencies, convert the spectrum back into an image.
In general, I advise you to read articles about the JPEG device and the discrete cosine transform on Habré. There were several articles that went into detail about all this and even experimented with other transformations / parameters / sampling tables / resampling ...

Answer 2

Why did you decide that you need filtering in the frequency domain? It's not at all obvious from your description. What do you want to get as a result?
If you want to experiment with pictures, then there is Imagemagick. This will eliminate the need to write code. https://legacy.imagemagick.org/Usage/fourier/
There are also examples of filtering in the frequency domain, such as typographic raster removal.
PS Gonzalez, Woods is a good book. :-)