How to find the percentage of n-gons overlapping a circle?

A

Alexander Razumov2016-06-09 15:05:03

Mathematics

Alexander Razumov, 2016-06-09 15:05:03

Good afternoon.
It is necessary to solve the following problem: there is one or several arbitrary n-gons (maybe not convex) that intersect with a circle. It is necessary to find the percentage of overlapping by n-gons of the circle. The coordinates of all points of the n-gon and the coordinates of the center of the circle and its radius are known. For clarity, a screenshot is attached.
I need a mathematical apparatus for this task. It is possible in English. It is possible in principle implementation on .
I know how to solve the problem of intersection of n-gons with each other. But not with a circle.
Thanks in advance.
Screen: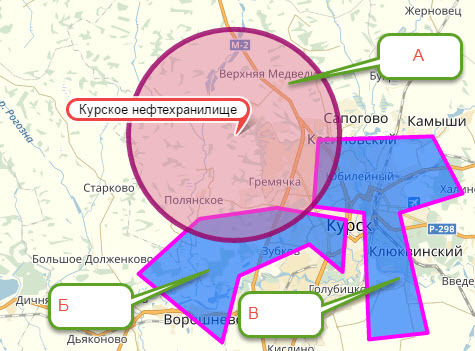

Reply

Answer the question

In order to leave comments, you need to log in

2 answer(s)

G

GreatRash, 2016-06-09
@GreatRash

https://www.geogebra.org/help/topic/intersection-a...

T

tsarevfs, 2016-06-09
@tsarevfs

Triangulate the polygon, solve the problem for each triangle. With a triangle, everything seems to be simple. We are looking for intersection points, we consider the area of \u200b\u200bthe segment + triangle / quadrilateral cut off by a chord.
For triangle ABC, you need to add the areas of the triangle (1) and the chords (2). For triangle BCD chord + quadrilateral.